题解 【NOIP2016】组合数问题

【NOIP2016】组合数问题

Description

Input

第一行有两个整数t, k，其中t代表该测试点总共有多少组测试数据，k的意义见【问题描述】。
接下来t行每行两个整数n, m，其中n, m的意义见【问题描述】。

Output

t行，每行一个整数代表所有的0<=i<=n,0<=j<=min(i,m)中有多少对(i, j)满足C(j,i)是k的倍数。

Sample Input

输入1：
1 2
3 3

输入2：
2 5
4 5
6 7

Sample Output

输出1：
1

输出2：
0
7

Hint

样例1提示：
在所有可能的情况中，只有C(1,2)是2的倍数。

输出范围：

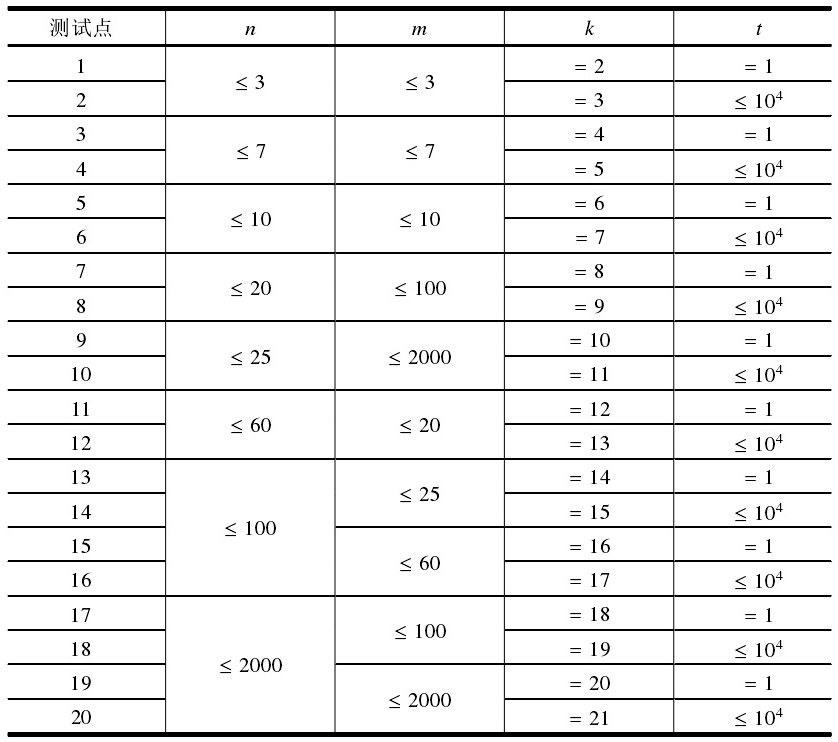
Source

NOIP2016 ，数学， 杨辉三角

解析

这题看上去确实很难做哈。

毕竟这数据范围。。

但实际上，我们完全可以利用杨辉三角预处理出组合数模k的值，

这样只要模k为0就是k的倍数了。

然后再O(2000*2000)记录下次数就能O(1)回答了。

上AC代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;

int t,k,m,n;
int f[][],a[][];

int main(){
    scanf("%d%d",&t,&k);
    for(int i=;i<=;i++){
        f[i][]=%k;
    }
    for(int i=;i<=;i++){
        for(int j=;j<=i;j++){
            f[i][j]=(ll)(f[i-][j]+f[i-][j-])%k;
        }
    }/*计算杨辉三角模k的值*/
    if(!f[][]) a[][]=;
    for(int i=;i<=;i++){
        a[i][]=a[i-][]+(f[i][]==);
        for(int j=;j<i;j++){
            a[i][j]=a[i-][j]+a[i][j-]-a[i-][j-]+(f[i][j]==);
            //如果值为0就是k的倍数
        }
        a[i][i]=a[i][i-]+(f[i][i]==);
        for(int j=i+;j<=;j++) a[i][j]=a[i][i];
    }/*预处理计数*/
    for(int i=;i<=t;i++){
        scanf("%d%d",&n,&m);
        printf("%d\n",a[n][m]);
        //O(1)回答
    }
    return ;
}