严格次小生成树[BJWC2010]

原文必点

 原题链接

题目描述

给定一张$N$ 个点$ M $条边的无向图，求无向图的严格次小生成树。

设最小生成树的边权之和为$sum$，严格次小生成树就是指边权之和大于$sum$的生成树中最小的一个。

输入格式

第一行包含两个整数$N$和$M$。

接下来$M$行，每行包含三个整数$x，y，z$，表示点$x$和点$y$之前存在一条边，边的权值为$z$。

输出格式

包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)

数据范围

\[N \le 10^5 \\\\
M \le 3*10^5
\]

输入样例：

输出样例：

解题报告

题意理解

要你构造一棵$n$个节点的严格次小生成树.

算法解析

分析条件

题目中给出的关键点,就是严格和次小.

什么是严格

就是题目强制要求严格单调性,不可以有$=$号的出现.

什么是次小

我们应该都知道,最小生成树,它要求边集合的边总和最小,那么次小生成树,要求边集合的边总和只比最小生成树边集合权值大.

总结性质

有至少一个（严格）次小生成树，和最小生成树之间只有一条边的差异。和真理只有一点差异,那就是出题人毒瘤

我们来粗略证明一下.(强行伪证)

我们知道最小生成树,是由$n-1$条构成的.

那么其他的$M-N+1$就是多余边.

假如说我们把一条多余边$(x,y,z)$,加入到了最小生成树中,那么一定会在$(x,y)$之间的路径上形成一个环.

那么这个环上面,最大的边称之为

\[Val_1
\]

次大的边,称之为

\[Val_2
\]

而且为了保证严格这个单调性质,我们必须设

\[Val_1>Val_2 \quad 最大的边一定大于次大的边
\]

接下来,我们就需要好好分析一下这条多余边了.

我们知道多余边,替换任何一条树上的一条边,都会使得最小生成树,不再最小

为什么?

因为最小生成树上的每一条边,一定是满足贪心性质下的最小的边.为什么啊?相信你的直觉啊

这个证明,我们使用的克鲁斯卡尔算法,已经告诉我们为什么.真相只有一个,我懒了

总而言之,言而总之,我们现在知道了这条多余边的加入.,一定会产生非最小生成树.

我们不妨令

\[ans=最小生成树边权之和
\]

假如说我们将多余边,替换掉最大权值边.

\[Val_1 ==> z \\\
此时我们发现当前生成树 W=ans+z-Val_1 \\\\
W=最小生成边权之和+加上多余边-最大权值边
\]

这一轮替换,我们可以认为这棵生成树有潜力成为次小生成树.

然后,我们发现,换一换次大边,也是可以的.

我们将多余边,强行替换掉次大权值边.

\[Val_2 ==> z \\\\
此时当前生成树 W=ans+z-Val_2 \\\\
W=最小生成树之和+加入多余边-次大权值边
\]

现在所有的候选生成树都出来了,但是我们面临一个非常严重的问题.

我们如何快速计算,一条路径上的最大边,和次大边.

动态规划

我们可以当前需要知道的状态,无非就是两个.

一条路径上的最大边
一条路径上的严格次大边

所以说,我们不妨就按照倍增数组的思路,去制造两个新数组.

最大边数组
严格次大边数组

\[f[x][k]=f[fa[x][k-1]][k-1]
\]

这是我们非常熟悉的Lca倍增数组.

然后咱们现在其实,手上掌握的最有力的性质,就是最值性质.

我们假设一条路径是由三段构造而成.

是三段,不是就三个点.

\[a=>c,c=>b,b=>a
\]

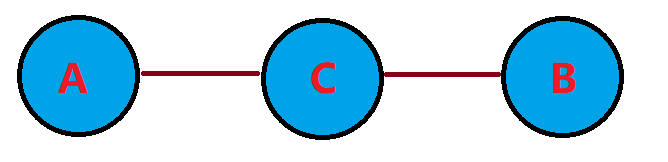
我们发现

\[A=>B的最大值其实等于 \\\\
max(A=>C最大值,B=>C最大值)
\]

这就是区间最值性质.

不过严格次大边,就比较麻烦了,不慌,咱们慢慢画图来.

为了下面简述方面,我们设置一下变量.

\[A=>C上最大边权为Val_{A,C} \quad 次大边权为V_{A,C} \\\\
C=>B上最大边权为Val_{B,C} \quad 次大边权为V_{B,C} \\\\
A=>B上最大边权为Val_{A,B} \quad 次大边权为V_{A,B} \\\\
\]

巧计一下,Val字母多,所以是最大边权,V字母少,所以是次大边权.

我们分类讨论一下,三种情况.

①第一段最大值=第二段最大值

\[Val_{A,C}=Val_{B,C}
\]

我们发现两段居然最大值一样.

次大边权就只能

\[V_{A,B}=max(V_{A,C},V_{B,C})
\]

②第一段最大值<第二段最大值.

那么此时,次大边权是可以取第一段最大值.

因为此时总段的最大值,一定是第二段最大值.

\[Val_{A,B}=Val_{B,C} \\\\
因此V_{A,B}可以=Val_{A,C}
\]

综上所述,我们总结下来就是.

\[V_{A,B}=max(Val_{A,C},V_{B,C})
\]

③第一段最大值>第二段最大值.

那么此时,次大边权是可以取第二段最大值.

因为此时总段的最大值,一定是第一段最大值.

\[Val_{A,B}=Val_{A,C} \\\\
因此V_{A,B}可以=Val_{B,C}
\]

同样,总结一下.

\[V_{A,B}=max(Val_{B,C},v_{A,B})
\]

然后我们将$A,B,C$具体化一下.

A其实就是起始节点.

C其实就是A跳跃了$2^{i-1}$格节点.

B其实就是A跳跃了$2^{i}$格节点.

广告时间:发现还是有点模糊,咱们的直播课会讲解的非常清晰,画图肯定少不了.

代码解析

#include <bits/stdc++.h>

using namespace std;

#define INF 1e16

const int N=1e5+200;

const int M=6*1e5+300;

int head[M],edge[M],Next[M],ver[M],tot,fa[M],n,m,father[N][32],deep[N];

long long dp[2][N][32],val1,val2,ans_max,ans;

struct node

{

    int x,y,z,vis;

} s[M];

int cmp(node a,node b)

{

    return a.z<b.z;

}

struct Edge

{

    void init2()

    {

        memset(head,0,sizeof(head));

        tot=0;

    }

    void add_edge(int a,int b,int c)

    {

        edge[++tot]=b;

        ver[tot]=c;

        Next[tot]=head[a];

        head[a]=tot;

    }

    int find(int x)

    {

        return x==fa[x]?x:fa[x]=find(fa[x]);

    }

    void Kruskal()

    {

        sort(s+1,s+1+m,cmp);

        for(int i=1; i<=m; i++)

        {

            int a=find(s[i].x),b=find(s[i].y);

            if (a==b)

                continue;

            s[i].vis=1;

            fa[a]=b;

            ans+=s[i].z;

            add_edge(s[i].x,s[i].y,s[i].z);

            add_edge(s[i].y,s[i].x,s[i].z);

        }

    }

    void bfs(int root)

    {

        deep[root]=0;

        queue<int> q;

        q.push(root);

        while(q.size())

        {

            int x=q.front(),len=(int)log2(deep[x]+1);

            q.pop();

            for(int i=head[x]; i; i=Next[i])

            {

                int y=edge[i];

                if(y==father[x][0])

                    continue;

                deep[y]=deep[x]+1;

                father[y][0]=x,dp[0][y][0]=ver[i],dp[1][y][0]=-INF;

                q.push(y);

                for(int t=1; t<=len; t++)

                {

                    father[y][t]=father[father[y][t-1]][t-1];

                    if(dp[0][y][t-1]!=dp[0][father[y][t-1]][t-1])

                    {

                        dp[0][y][t]=max(dp[0][y][t-1],dp[0][father[y][t-1]][t-1]);

                        dp[1][y][t]=min(dp[0][y][t-1],dp[0][father[y][t-1]][t-1]);

                    }

                    else

                    {

                        dp[0][y][t]=dp[0][y][t-1];

                        dp[1][y][t]=max(dp[1][y][t-1],dp[1][father[y][t-1]][t-1]);

                    }

                }

            }

        }

    }

    inline void update2(int x)

    {

        if(x>val1)

            val2=val1,val1=x;

        else if(x>val2 && x!=val1)

            val2=x;

    }

    inline void update(int x, int t)

    {

        update2(dp[0][x][t]);

        update2(dp[1][x][t]);

    }

    inline void Lca(int x, int y)

    {

        val1=val2=-INF;

        if(deep[x]<deep[y])

            swap(x,y);

        while(deep[x]>deep[y])

        {

            int t=(int)log2(deep[x]-deep[y]);

            update(x,t),x=father[x][t];

        }

        if(x==y)

            return;

        for(int t=(int)log2(deep[x]); t>=0; t--)

        {

            if(father[x][t]!=father[y][t])

            {

                update(x,t),update(y,t);

                x=father[x][t];

                y=father[y][t];

            }

        }

        update(x,0),update(y,0);

    }

} g1;

int main()

{

//	freopen("stdin.in","r",stdin);

//	freopen("stdout.out","w",stdout);

    scanf("%d%d",&n,&m);

    g1.init2();

    for(int i=1; i<=m; i++)

    {

        int a,b,c;

        scanf("%d%d%d",&a,&b,&c);

        s[i].x=a,s[i].y=b,s[i].z=c;

        fa[i]=i;

    }

    g1.Kruskal();

    g1.bfs(1);

    ans_max=INF;

    for(int i=1; i<=m; i++)

    {

        if(!s[i].vis)

        {

            g1.Lca(s[i].x,s[i].y);

            if(val1!=s[i].z)

                ans_max=min(ans_max,ans-val1+s[i].z);

            else

                ans_max=min(ans_max,ans-val2+s[i].z);

        }

    }

    printf("%lld\n",ans_max);

    return 0;

}