CF C.Ivan the Fool and the Probability Theory【思维·构造】

题目传送门

题目大意：

一个$n*m$的网格图，每个格子可以染黑色、白色，问每个格子最多有一个相邻格子颜色相同的涂色方案数
$n,m<=1e5$

分析：

首先，考虑到如果有两个相邻的格子颜色相同，那么这两行/列的格子状态就确定了。比如：

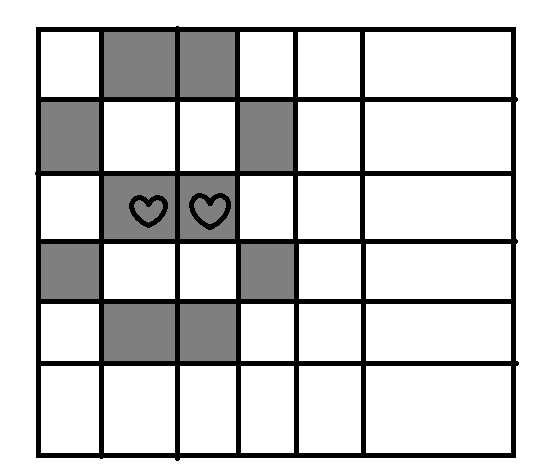
在中间两个爱心格子被确定的情况下，第二列和第三列的涂色情况就已经被确定了。实际上，第一列和第四列涂的颜色也确定了。（最后这句话我们留着待会儿分析）

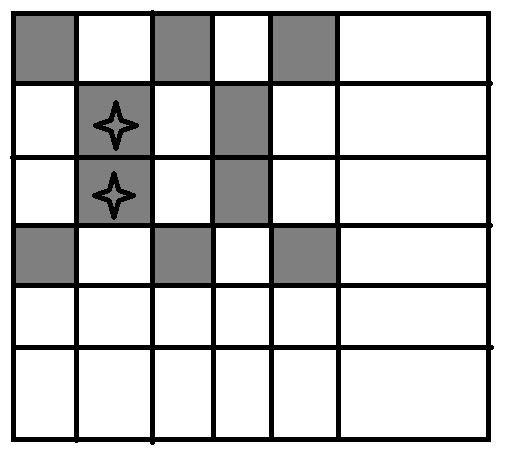
同理，在中间两个星星确定的时候，第二行和第三行的涂色情况也唯一确定。实际上，第一行和第四列涂的颜色也确定了。

---

假如说在一个方格中，既有横着出现的两个连续的一样颜色的格子，也有竖着出现的两个连续的一样颜色的格子，就像这样：

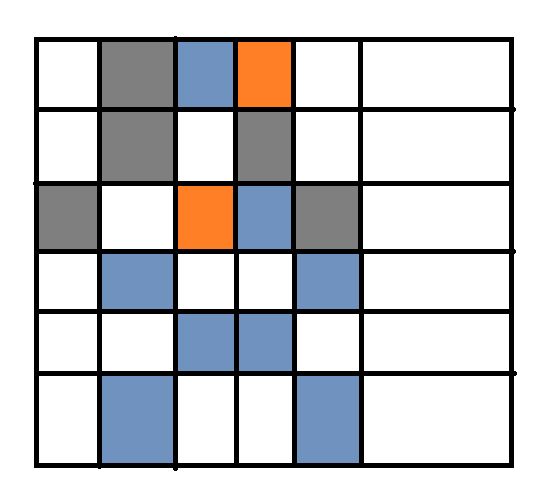
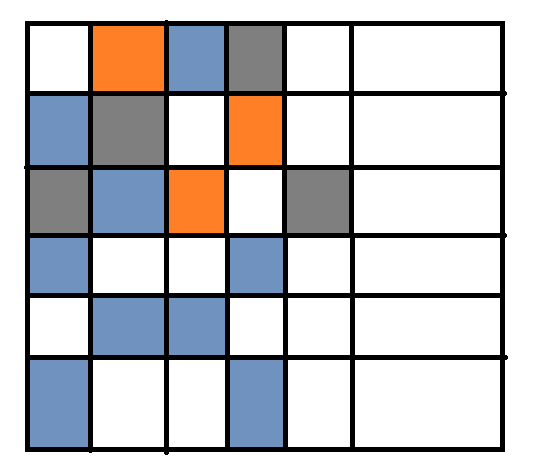
那么一定会产生矛盾，无论怎么挪都会产生矛盾。（橙色的部分是既需要用灰色，也需要用蓝色涂的格子，是矛盾的地方）

所以，在一种着色方案中，这种相邻两个颜色一样的情况只会在一个方向中出现，我们只需要考虑一个方向那么多行的方案数，另外一个方向的同理就好。

---

如果已经确定相邻两个颜色一样的格子出现的方向（为方便讨论，下面我们假设这两个格子是竖着的），那么每一行的格子颜色一定是交错的，两行之间要么一样，要么颜色相反，而且颜色一样的不能连着出现3次及以上。

在第一行确定的情况下，如果要求每一个格子的每个相邻格子的颜色都和他不一样，那么这是一个棋盘染色，就唯一确定了。

但是，按照这道题的条件来说的话，后面的格子可以有两行，也可以只有一行。（就是一次性确定两行或一次性确定一行）

Like this:

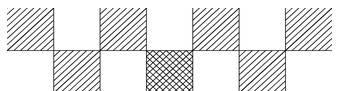
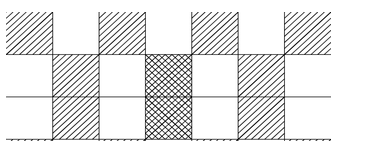
设$f[i]$表示铺到第$i$行（前$i$行）的方案总数，那么递推式就是$f[i]=f[i-1]+f[i-2]$

（初始化$f[0]=1$是一开始就是两行连着一样的情况）

答案就是$f[n]$。

然后，还有相邻两个颜色一样的格子是竖着的，方案数就是$f[m]$，这两类在前面已经说过没有交集，答案就是$f[n]+f[m]$

然后，棋盘染色的情况在两种情况中都被计算了，所以答案要减1。

最后，黑白颜色可以反过来，所以乘2.

做完了，$Nice!$

 /*
 ID: Starry21
 */
 #include<iostream>
 #include<string>
 #include<cstdio>
 #include<cstring>
 #include<map>
 #include<algorithm>
 using namespace std;
 #define N 100005
 #define ll long long
 #define MOD 1000000007
 int n,m;
 ll f[N];
 int main()
 {
     scanf("%d %d",&n,&m);
     f[]=f[]=;
     for(int i=;i<=max(n,m);i++)
         f[i]=(f[i-]+f[i-])%MOD;
     printf("%lld\n",*((f[n]+f[m])%MOD-+MOD)%MOD);
     return ;
 }

代码贼短