QR分解迭代求特征值——原生python实现(不使用numpy)

QR分解：

有很多方法可以进行QR迭代，本文使用的是Schmidt正交化方法

具体证明请参考链接 https://wenku.baidu.com/view/c2e34678168884868762d6f9.html

迭代格式

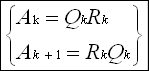
实际在进行QR分解之前一般将矩阵化为上hessnberg矩阵（奈何这个过程比较难以理解，本人智商不够，就不做这一步了哈哈哈）

迭代终止条件

看了很多文章都是设置一个迭代次数，感觉有些不是很合理，本来想采用A(k+1)-A(k)的对角线元素的二范数来作为误差的，但是我有没有一些严格的证明，所以本文也采用比较大众化的思路，设置迭代次数。

Python实现

 M = [[2, 4, 2], [-1, 0, -4], [2, 2, 1]]

 import copy
 import math

 class QR(object):

     def __init__(self, data):
         self.M = data
         self.degree = len(data)

     def get_row(self, index):
         res = []
         for i in range(self.degree):
             res.append(self.M[i][index])
         return res

     def get_col(self, index):
         res = []
         for i in range(self.degree):
             res.append(self.M[i][index])
         return res

     @staticmethod
     def dot(m1, m2):
         res = 0
         for i in range(len(m1)):
             res += m1[i] * m2[i]
         return res

     @staticmethod
     def list_multi(k, lt):
         res = []
         for i in range(len(lt)):
             res.append(k * lt[i])
         return res

     @staticmethod
     def one_item(x, yArr):
         res = [0 for i in range(len(x))]
         temp_y_arr = []

         n = len(yArr)
         if n == 0:
             res = x
         else:
             for item in yArr:
                 k = QR.dot(x, item) / QR.dot(item, item)
                 temp_y_arr.append(QR.list_multi(-k, item))
             temp_y_arr.append(x)

             for item in temp_y_arr:
                 for i in range(len(item)):
                     res[i] += item[i]
         return res

     @staticmethod
     def normal(matrix):
         yArr = []
         yArr.append(matrix[0])

         for i in range(1, len(matrix)):
             yArr.append(QR.one_item(matrix[i], yArr))
         return yArr

     @staticmethod
     def normalized(lt):
         res = []
         sm = 0
         for item in lt:
             sm += math.pow(item, 2)
         sm = math.sqrt(sm)
         for item in lt:
             res.append(item / sm)
         return res

     @staticmethod
     def matrix_T(matrix):
         mat = copy.deepcopy(matrix)
         m = len(mat[0])
         n = len(mat)
         for i in range(m):
             for j in range(n):
                 if i < j:
                     temp = mat[i][j]
                     mat[i][j] = mat[j][i]
                     mat[j][i] = temp
         return mat

     @staticmethod
     def matrix_multi(mat1, mat2):
         res = []
         rows = len(mat1[0])
         cols = len(mat1)
         for i in range(rows):
             temp = [0 for i in range(cols)]
             res.append(temp)

         for i in range(rows):
             for j in range(cols):
                 sm = 0
                 for k in range(cols):
                     sm += (mat1[k][i] * mat2[j][k])
                 res[j][i] = sm
         return res

     def execute(self):
         xArr = []
         for i in range(self.degree):
             xArr.append(self.get_col(i))
         yArr = QR.normal(xArr)
         self.Q = []
         for item in yArr:
             self.Q.append(QR.normalized(item))

         self.R = QR.matrix_multi(QR.matrix_T(self.Q), xArr)
         return (self.Q, self.R)

 # A = [
 #     [1, 0, -1, 2, 1],
 #     [3, 2, -3, 5, -3],
 #     [2, 2, 1, 4, -2],
 #     [0, 4, 3, 3, 1],
 #     [1, 0, 8, -11, 4]
 # ]
 # A = [
 #     [1, 2, 2],
 #     [2, 1, 2],
 #     [2, 2, 1]
 # ]
 A = [
     [3, 2, 4],
     [2, 0, 2],
     [4, 2, 3]
 ]

 temp = copy.deepcopy(A)
 val = []  # 特征值
 times = 20  # 迭代次数
 for i in range(times):
     qr = QR(temp)
     (q, r) = qr.execute()
     temp = QR.matrix_multi(r, q)
     temp = QR.matrix_T(temp)

 for i in range(len(temp)):
     for j in range(len(temp[0])):
         if i == j:
             val.append(temp[i][j])
 # 特征值
 print(val)

结果展示

总结

使用QR分解迭代求特征值，收敛的比较快，也可以求出所有的特征值，但是如果要求特征向量的话，还是需要求解线性方程组（感觉很麻烦）