POJ3321[苹果树] 树状数组/线段树 + dfs序

Apple Tree

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions:39452		Accepted: 11694

Description

There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

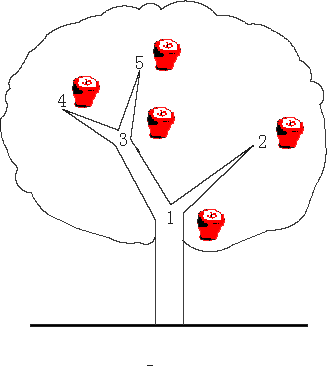
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.

Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1

Sample Output

3
2

Source

树状数组

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=,maxm=;
int n,m,Time,tot,lnk[maxn],son[maxm],nxt[maxm],in[maxn],out[maxn];
bool vis[maxn];
struct BLT
{
    int c[maxn];
    void Clear(){memset(c,,sizeof(c));}
    int Lowbit(int x){return x&(-x);}
    void Add(int x,int da){while (x<=n) c[x]+=da,x+=Lowbit(x);}
    int Get(int x){int sum=; while (x) sum+=c[x],x-=Lowbit(x); return sum;}
}tr;//树状数组
inline int Read()
{
    int res=;
    char ch=getchar();
    while (ch<''||ch>'') ch=getchar();
    while (ch>=''&&ch<='') res=res*+ch-,ch=getchar();
    return res;
}
void Dfs(int x,int fa)
{
    in[x]=++Time;
    for (int j=lnk[x]; j; j=nxt[j])
     if (son[j]!=fa) Dfs(son[j],x);
    out[x]=Time;
}
void Add_e(int x,int y)
{
    son[++tot]=y; nxt[tot]=lnk[x]; lnk[x]=tot;
}
int main()
{

    n=Read(); Time=;
    for (int i=,x,y; i<n; i++) x=Read(),y=Read(),Add_e(x,y),Add_e(y,x);
    Dfs(,); m=Read(); tr.Clear();
    for (int i=; i<=n; i++) tr.Add(i,);
    memset(vis,,sizeof(vis));
    for (int i=; i<=m; i++)
    {
        char ch=getchar();
        while (ch!='Q'&&ch!='C') ch=getchar();
        int x=Read();
        if (ch=='Q') printf("%d\n",tr.Get(out[x])-tr.Get(in[x]-));
         else {if (vis[x]) tr.Add(in[x],); else tr.Add(in[x],-); vis[x]=-vis[x];}
    }
    return ;
}

线段树

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <vector>

using namespace std;

#define begin Begin
#define next Next

#define REP(i, a, b) for (int i = (a), _end_ = (b); i <= _end_; ++i)
#define EREP(i, a) for (int i = begin[a]; ~i; i = next[i])
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define mp make_pair
#define x first
#define y second
#define pb push_back
#define SZ(x) (int((x).size()))
#define ALL(x) (x).begin(), (x).end()

template<typename T> inline bool chkmin(T &a, const T &b){ return a > b ? a = b,  : ; }
template<typename T> inline bool chkmax(T &a, const T &b){ return a < b ? a = b,  : ; }

typedef long long LL;

const int dmax =  << , oo = 0x3f3f3f3f;

int n, m;

int begin[dmax], to[dmax], next[dmax], e;

int d[dmax], size[dmax], dis;

int c[dmax];

inline void init()
{
    e = dis = ;
    memset(begin, -, sizeof begin);
}

inline void add(int x, int y)
{
    to[++e] = y;
    next[e] = begin[x];
    begin[x] = e;
}

void dfs(int x, int fa)
{
    size[x] = ;
    d[x] = ++dis;
    EREP(i, x)
        if (to[i] == fa) continue;
        else
        {
            dfs(to[i], x);
            size[x] += size[to[i]];
        }
}

#define left x << 1, l, mid
#define right x << 1 | 1, mid + 1, r

template<typename T> inline T Mid(const T &x, const T &y){ return (x + y) >> ; }

inline void push_up(int x){ c[x] = c[x << ] + c[x <<  | ]; }

void create(int x, int l, int r)
{
    if (l == r)
    {
        c[x] = ;
        return;
    }
    int mid = Mid(l, r);
    create(left);
    create(right);
    push_up(x);
}

int query(int x, int l, int r, int s, int t)
{
    if (l >= s && r <= t)
        return c[x];
    int mid = Mid(l, r);
    int sum = ;
    if (s <= mid)
        sum += query(left, s, t);
    if (t > mid)
        sum += query(right, s, t);
    return sum;
}

void update(int x, int l, int r, int t)
{
    if (l == r)
    {
        c[x] ^= ;
        return;
    }
    int mid = Mid(l, r);
    if (t <= mid)
        update(left, t);
    else update(right, t);
    push_up(x);
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("input.txt", "r", stdin);
    freopen("output.txt", "w", stdout);
#endif
    while (scanf("%d", &n) != EOF)
    {
        init();

        REP(i, , n - )
        {
            int x, y;
            scanf("%d%d", &x, &y);
            add(x, y);
            add(y, x);
        }
        dfs(, -);
        create(, , n);
        scanf("%d", &m);
        getchar();
        REP(i, , m){
            char c = getchar();
            int x;
            scanf("%d", &x);
            if (c == 'Q')
                printf("%d\n", query(, , n, d[x], d[x] + size[x] - ));
            else update(, , n, d[x]);
            getchar();
        }
    }
    return ;
}