树链剖分

http://www.lydsy.com/JudgeOnline/problem.php?id=1036

https://oi.men.ci/tree-chain-split-notes/、

点分治

https://oi.men.ci/tree-divide-notes/

https://www.luogu.org/blog/chengni5673/dian-fen-zhi

对于一棵树，统计长度为 x 的路径的路径数.

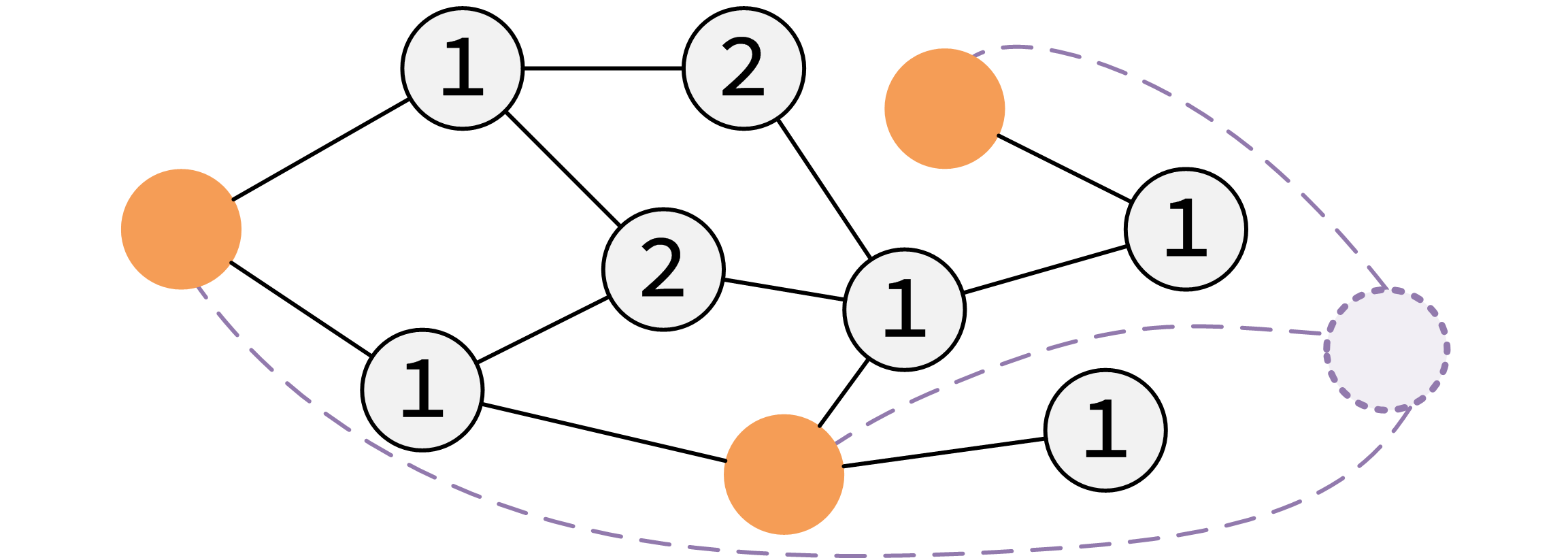
点分治: 找到一个点为根，统计答案，然后将它的子树分离，分别进行同样的操作，继续，直到只剩下一个点. 其中选择的根是有要求的，为了保证时间复杂度，我们需要尽量的让子树的大小相近，所以每一次我们选择的根都最好是当前这棵树的重心.

图论常见技巧

  • 反向建边
  • 虚点连边

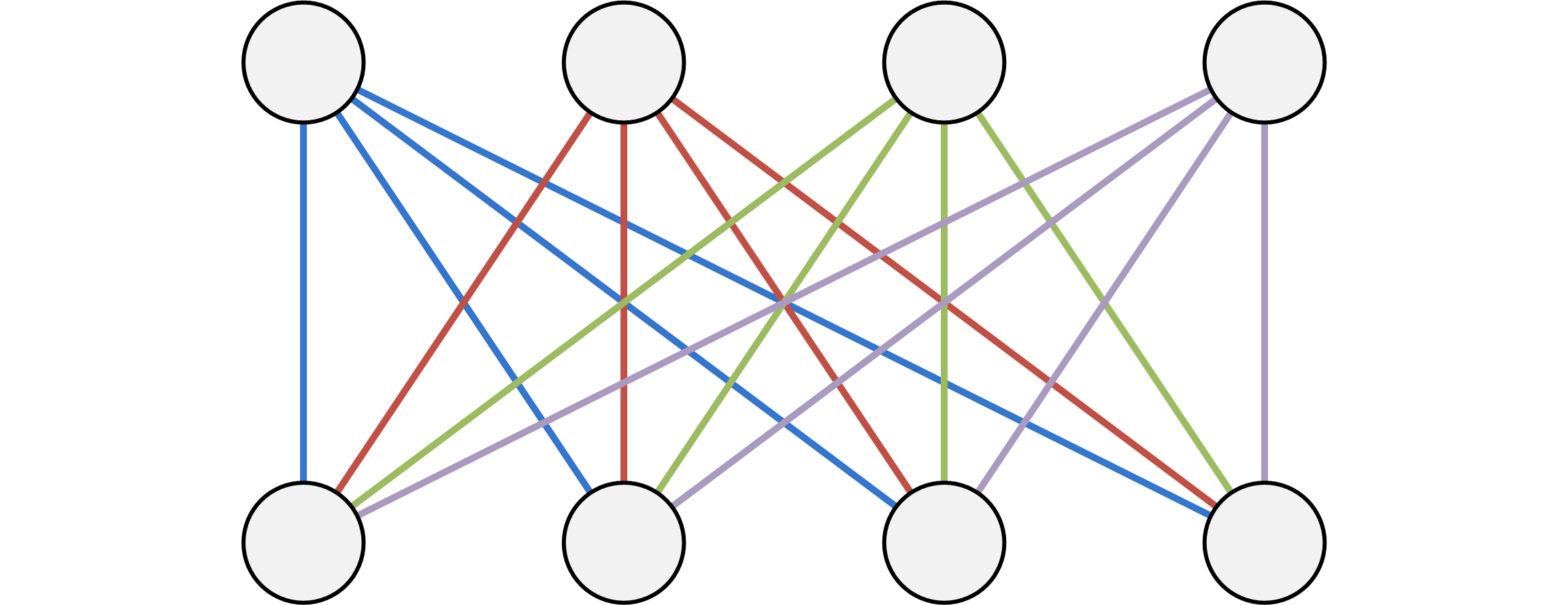
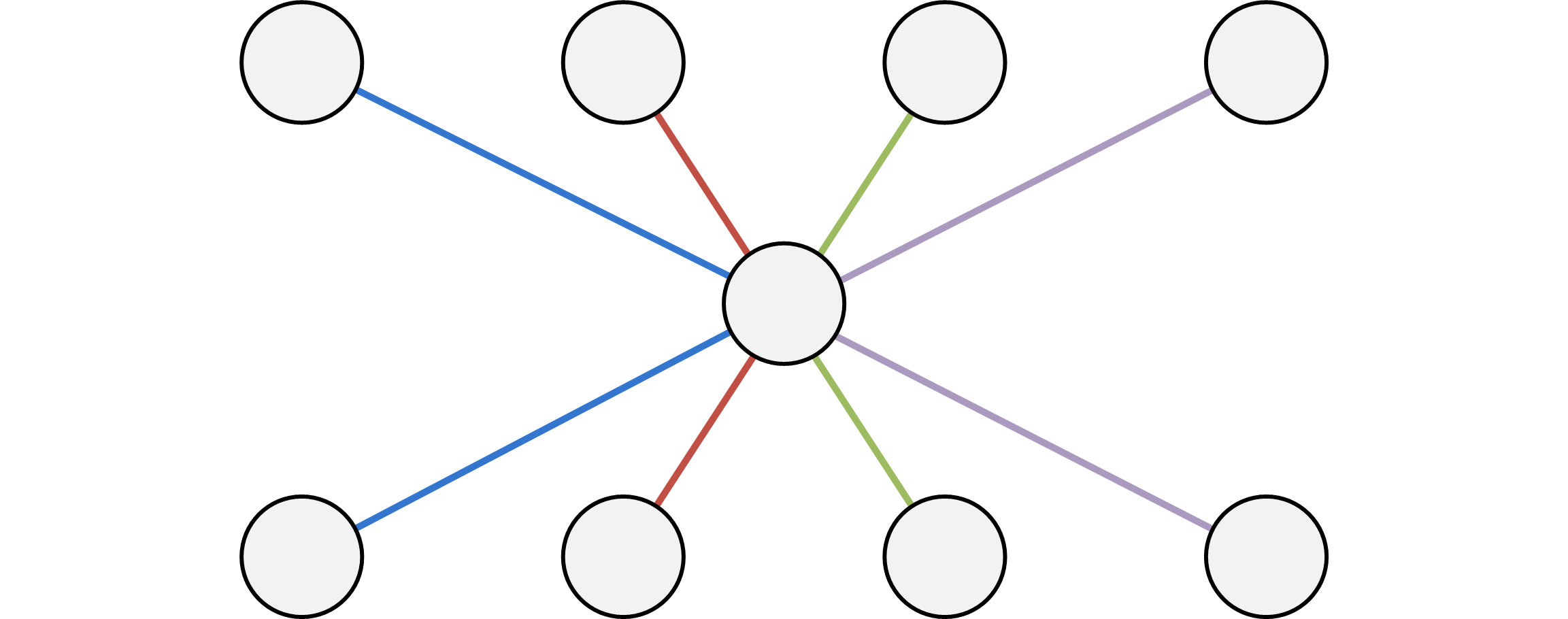
Graph 1. 求各点到指定点集的最短距离的优化方法

(a)

(b)

Graph 2. 二分完全图建边的优化方法

  • 建边的线段树优化

Graph 3. 建边的线段树优化

  • 拆点
  • 分层图解决刁钻图上操作

分层图就是有多维状态的有边长图，比起正常的最短路转移多了一种跨维度转移的状态转移. 一般都是舍去某边长度，最多舍多少次 (次数较少).

[JLOI2011] 飞行路线: Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务，设这些城市分别标记为 0 到 n-1，一共有 m 种航线，每种航线连接两个城市，并且航线有一定的价格。Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 k 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？

分层图可以很巧妙的解决这个问题. 想象你每次使用免费航线之前和之后分别存在于不同的时空 (不同的层) 里面，每使用一次免费航线，你就从这个时空进入了另一个时空 (免费). 根据以上思想建图，一共建 k+1 层图，相邻的两层图中进行连边 (单向边，距离为 1). 然后跑 Dijkstra 即可.

— gaotianyu1350

图论的注意点

  • 无向图/有向图
  • 自环、重边
  • 环（缩点）
  • 负环、零环

13 October的更多相关文章

  1. centos各版本信息

    CentOS version Architectures RHEL base Kernel CentOS release date RHEL release date Delay (days) 2.1 ...

  2. Android学习系列(39)--Android主题和样式之系统篇（上）

    [基于最新的Android4.4的源码分析] 每家公司或者每个移动团队无不想开发出一套自己的UI框架,融入自己的设计和特性,这必然会去修改android的ui.所以,学习和理解android的UI设计 ...

  3. CentOS和Redhat发行版linux内核版本的对应关系

    由于Redhat和CentOS的发行版本现在众多,所以我们应该知道CentOS和Redhat及linux内核之间版本的对应关系对维护系统还是很有帮助的.对应的列表如下: Redhat 9.0————— ...

  4. 支持不同Android设备，包括：不同尺寸屏幕、不同屏幕密度、不同系统设置

    Some of the important variations that you should consider include different languages, screen sizes, ...

  5. xmlhttp

    File an issue about the selected textFile an issue about the selected text XMLHttpRequest Living Sta ...

  6. Fix catalyst driver in Ubuntu 13.04 / 13.10

    Fix catalyst driver in Ubuntu 13.04 / 13.10(墙外文章备份) 1. Introduction I found lots of people strugglin ...

  7. 【13】python time时间模块知识点备查

    表示时间的三种形式 # 时间模块 '''UTC(世界协调时间):格林尼治天文时间,世界标准时间,在中国来说是UTC+8DST(夏令时):是一种节约能源而人为规定时间制度,在夏季调快1个小时 时间的表示 ...

  8. Ural State University Internal Contest October'2000 Junior Session

    POJ 上的一套水题,哈哈~~~,最后一题很恶心,不想写了~~~ Rope Time Limit: 1000MS   Memory Limit: 65536K Total Submissions: 7 ...

  9. Leetcode problems classified by company 题目按公司分类(Last updated: October 2, 2017)

    All LeetCode Questions List 题目汇总 Sorted by frequency of problems that appear in real interviews. Las ...

随机推荐

  1. DT时代，企业更需构建精准数据分析体系

    DT时代,企业更需构建精准数据分析体系 随着互联网的飞速发展,信息的传输日益方便快捷,需求也日益突出,纵观整个互联网领域,大数据已被认为是继云计算.物联网之后的又一大颠覆性的技术性革命,毋庸置疑,大数 ...

  2. C# Thread3——前台线程后台线程

    默认情况下,显示创建的线程都是前台线程,进程会等待内部所有的前台线程执行完才会结束退出 1.默认创建的线程都是前台线程 2.进程会等待所有的前台线程执行完而结束,如果还存在后台线程则会强行中断并且退出 ...

  3. python爬虫——爬取淘票票正在热映电影

    今天正好学习了一下python的爬虫,觉得收获蛮大的,所以写一篇博客帮助想学习爬虫的伙伴们. 这里我就以一个简单地爬取淘票票正在热映电影为例,介绍一下一个爬虫的完整流程. 首先,话不多说,上干货——源 ...

  4. python控制流-导入模块

    一.模块 1.含义 Python 程序可以调用一组基本的函数,这称为“内建函数”,包括你见到过的 print().input()和 len()函数.Python 也包括一组模块,称为“标准库”.每个模 ...

  5. idea 社区版本创建javaweb项目 使用jetty

    idea社区版本 创建javaweb项目后使用jetty启动 <dependencies> <dependency> <groupId>javax.servlet& ...

  6. javascript数组排序和prototype详解

    原型的概念::原型对象里的所有属性和方法 被所有构造函数实例化出来的对象所共享,类似于java中的 static 正因为共享所以单一的操作 就会影响了全局,因此使用时需注意 基于prototype:为 ...

  7. py基础

    基本语句和函数等练习,知识点都在代码里... """ a = int(input('a = ')) b = int(input('b = ')) print('%d + ...

  8. Java学习day8面向对象编程2-类的属性和方法

    一.类的属性 1.语法格式 修饰符 类型 属性名 = 初值 说明:修饰符private:该属性只能由该类的方法使用.在同一类内可见.使用对象:变量.方法. 注意:不能修饰类(外部类)    修饰符pu ...

  9. BitMap的原理和实现

    相关概念 基础类型 在java中: byte -> 8 bits -->1字节 char -> 16 bit -->2字节 short -> 16 bits --> ...

  10. 2019 Multi-University Training Contest 2 - 1009 - 回文自动机

    http://acm.hdu.edu.cn/showproblem.php?pid=6599 有好几种实现方式,首先都是用回文自动机统计好回文串的个数. 记得把每个节点的cnt加到他的fail上,因为 ...