[BJOI2006]狼抓兔子（网络流）

题目描述

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

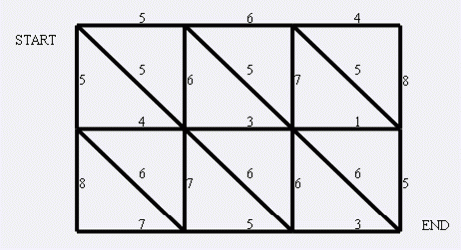
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

输入输出格式

输入格式：

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

输出格式：

输出一个整数，表示参与伏击的狼的最小数量.

输入输出样例

输入样例#1：

3 4

5 6 4

4 3 1

7 5 3

5 6 7 8

8 7 6 5

5 5 5

6 6 6

输出样例#1：

14

这道题算是网络流的水题吧，看到要把兔子全部阻截掉基本上可以考虑到网络流了。

其实这道题是要我们求最小割

由最大流=最小割（证明网上有）

直接跑最大流即可。

建边看似麻烦实际上冷静下来慢慢想其实很简单了。

需要注意的是这张图是无向图，我们把两条边的初始流量都见成\(v\)就可以了

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0') {if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*w;
}
int n,m,cnt=1,s,t;
int inf=2000000000;
int head[1000001],team[1000001],deep[1000001];
struct node{
int to,next,v;
}edge[6000001];
void add(int x,int y,int v)
{
    cnt++;
    edge[cnt].to=y;
    edge[cnt].next=head[x];
    edge[cnt].v=v;
    head[x]=cnt;
}
bool bfs();
int dfs(int,int);
int main()
{
    int x;
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<m;j++)
        {
            x=read();
            add((i-1)*m+j,(i-1)*m+j+1,x);
            add((i-1)*m+j+1,(i-1)*m+j,x);
        }
    }
    for(int i=1;i<n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            x=read();
            add((i-1)*m+j,i*m+j,x);
            add(i*m+j,(i-1)*m+j,x);
        }
    }
    for(int i=1;i<n;i++)
    {
        for(int j=1;j<m;j++)
        {
            x=read();
            add((i-1)*m+j,i*m+j+1,x);
            add(i*m+j+1,(i-1)*m+j,x);
        }
    }
    s=1;t=n*m;
    int ans=0;
    while(bfs())
    {
        int d;
        while(d=dfs(s,inf))
        {
            ans+=d;
        }
    }
    printf("%d",ans);
}
bool bfs()
{
    int u,v,l=0,r=1;
    memset(deep,0,sizeof(deep));
    memset(team,0,sizeof(team));
    team[1]=s;deep[s]=1;
    while(l<r)
    {
        l++;
        u=team[l];
        for(int i=head[u];i;i=edge[i].next)
        {
            v=edge[i].to;
            if(!deep[v]&&edge[i].v>0)
            {
                r++;
                deep[v]=deep[u]+1;
                team[r]=v;
            }
        }
    }
    if(!deep[t]) return false;
    return true;
}
int dfs(int k,int v)
{
    //cout<<k<<".."<<endl;
    if(k==t) return v;
    int u,d;
    for(int i=head[k];i;i=edge[i].next)
    {
        u=edge[i].to;
        if(deep[u]==deep[k]+1&&edge[i].v>0)
        {
            d=dfs(u,min(edge[i].v,v));
            if(d>0)
            {
                edge[i].v-=d;
                edge[(i^1)].v+=d;
                return d;
            }
        }
    }
    if(d==0) deep[k]=0;
    return 0;
}