正规式->最小化DFA说明

 

整体的步骤是三步：
一，先把正规式转换为NFA（非确定有穷自动机）,
二，在把NFA通过“子集构造法”转化为DFA，
三，在把DFA通过“分割法”进行最小化。

一步很简单，就是反复运用下图的规则，图1

这样就能转换到NFA了。
给出一个例题，来自Google book。本文主要根据这个例题来讲，图2

二.子集构造法。
同样的例题，把转换好的NFA确定化，图3

这个表是从NFA到DFA的时候必须要用到的。第一列第一行I的意思是从NFA的起始节点经过任意个ε所能到达的结点集合。Ia表示从该集合开始经过一个a所能到达的集合，经过一个a的意思是可以略过前后的ε。同样Ib也就是经过一个b，可以略过前后任意个ε。
至于第二行以及后面的I是怎么确定的。我参考了一些题目才明白，原来就是看上面的Ia和Ib哪个还没出现在I列，就拿下来进行运算，该列对应的Ia和Ib就是前面我说的那样推导。

如果还不太明白，看图就是了。你会发现I中的几个项目都在Ia和Ib中出现了。而且是完全出现

这步做完以后，为了画出最后的DFA，那么肯定得标出一些号来，比如1.2.3.。或者A。 B。c，我一般标的方法是先把I列全部标上1.2.3.递增。然后看1表示的集合和Ia和Ib中的哪个集合一样，就把那个集合也表示为1.继续向下做。最后会得到这样一个表格。图4

至此，就可以表示出DFA了。就对照上面那个表，从0节点开始经过a到1.经过b到2，就这样画就行了。。

最后的DFA如下图，图5

双圈的表示终态，这个是怎么来的呢。去看看图4，会发现有些项之前有双圈标志，这个是因为在NFA图2中，9为终态，所以所有包含9的集合都被认为是终态集，改成1.2.3.。。方便画节点后就需要把这些点作为终态了。。

三.最小化，分割法。

FA的最小化就是寻求最小状态DFA

最小状态DFA的含义:
1.没有多余状态(死状态)

 

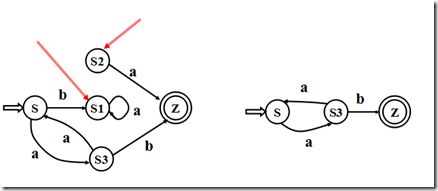
除多余状态
什么是多余状态？
从这个状态没有通路到达终态；S1
从开始状态出发，任何输入串也不能到达的那个状态。S2
如何消除多余状态？
删除

2. 没有两个状态是互相等价（不可区别）
两个状态s和t等价的条件：
兼容性（一致性）条件——同是终态或同是非终态
传播性（蔓延性）条件——对于所有输入符号，状态s和状态t必须转换到等价的状态里。。

DFA的最小化—例子，第一步都是固定的。分成终态和非终态

１．将Ｍ的状态分为两个子集一个由终态k1=｛Ｃ，Ｄ，Ｅ，Ｆ｝组成，一个由非终态k2=｛Ｓ，Ａ，Ｂ｝组成，

２．考察｛Ｓ，Ａ，Ｂ｝是否可分．

因为Ａ经过a到达C属于k1.而S经过a到达A属于k2.B经过a到达A属于k2，所以K2继续划分为{S，B},{A},

３．考察｛Ｓ，Ｂ｝是否可再分：

B经过b到达D属于k1.S经过b到达B属于k2，所以S，B可以划分。划分为{S},{B}

４．考察｛Ｃ，Ｄ，Ｅ，Ｆ｝是否可再分：
因为Ｃ，Ｄ，Ｅ，Ｆ经过a和b到达的状态都属于｛Ｃ，Ｄ，Ｅ，Ｆ｝=k1所以相同，所以不可再分：

５．｛Ｃ，Ｄ，Ｅ，Ｆ｝以｛Ｄ｝来代替则，因为CDEF相同，你也可以用C来代替。无所谓的最小化的ＤＦＡ如图，：