SVD 学习笔记

本文主要学习了这篇博客：http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html，将SVD讲的恨透，特征值讲的也非常好。

特征值

矩阵分解时可以将矩阵用一组两两正交的基表示，也就是一组特征向量，而特征值就是表示每个特征向量的重要程度的数值。

奇异值

特征值是对方阵来说的，对于非方阵我们该怎么办呢，我们仿照特征分解，就有了下面的式子

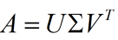
假设A是一个M*N的矩阵，那么得到的U是一个M * M的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个M *N的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个N * N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），从图片来反映几个相乘的矩阵的大小可得下面的图片(PS:下图中用颜色方块的形状大概表示矩阵的形状)

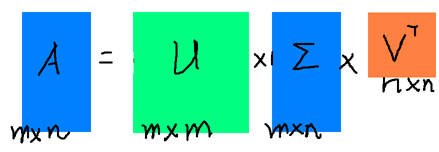
而关于奇异值的具体求解，wikipedia 上讲的还是很好的。

注：一下为特异值的求解

对于任意的奇异值分解，矩阵Σ的对角线上的元素等于M的奇异值. U和V的列分别是奇异值中的左、右奇异向量。

奇异值分解在意义上看很一般，因此它可以适用于任意m×n矩阵，而特征分解只能适用于特定类型的方阵。不过，这两个分解之间是有关联的。 给定一个M的奇异值分解，根据上面的论述，两者的关系式如下：

关系式的右边描述了关系式左边的特征值分解。于是：

• V（右奇异向量）的列是的特征向量。
• U（左奇异向量）的列是的特征向量。
• Σ（非零奇异值）的非零元素是或者中非零特征值的平方根。

奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子：

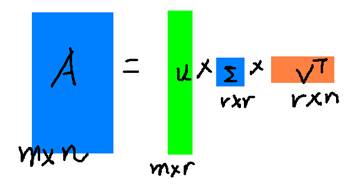
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

好，到这里SVD就相当于讲完了，其核心思想就一点用前10%甚至1%的奇异值表示了全部的奇异值，因为在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了，这样做可以大大的减少数据的存储和计算。