寻找一组数中最大的K个数

对于"从一组数中挑出最大的K个数"这个在面试中经常会遇到，所以这次好好的去解析它，而当拿到这个问题时第一时间能想到解法就是：先对数据进行排序，然后再取最大的K个元素，当然这思路没毛病，但是对于数据量非常大(如：一万个数)的情况是不是先对它进行排序的代价太高了，有木有比较优的解法呢？当然有，那就是采用上篇学习到的利用二叉堆排序去解决。

定义二叉堆结构：

首先是需要用代码去实现一个堆这样的数据结构，而堆的特性在上篇【http://www.cnblogs.com/webor2006/p/7685197.html】中已经有介绍了，下面直接实现，先定义框架：

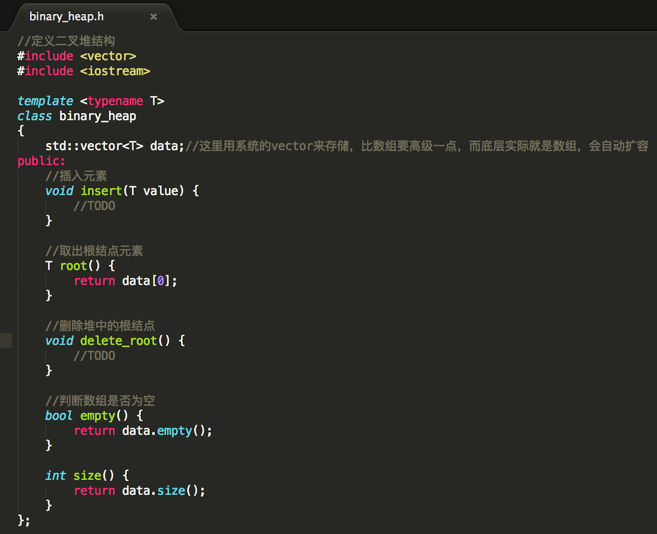
其中核心就是实现数据的插入和删除，这个整个思想已经在之前介绍堆时介绍过了，这里就不多阐述了，下面来分别实现：

①、insert():插入元素

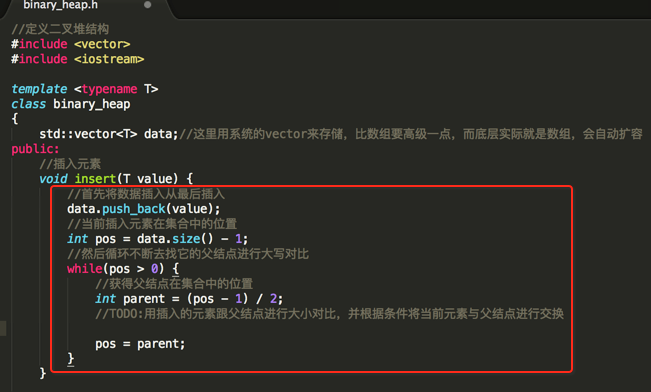
其中怎么根据当前结点得到它的父结点的公式是：int parent = (pos - 1) / 2；猭由是根据父节点可以计算得到它左右子节点的位置，公式如：

上面公式是在上篇对堆的理论上有详细说明，而其中的i就是父元素的位置，所以其推导过程，拿左子节点为例：

因为：子节点位置 = 2 * 父结点位置 + 1

所以：父结点位置parent = (子节点位置pos - 1) / 2

接下来实现关键的对比部份，由于堆有小堆跟大堆，如下：

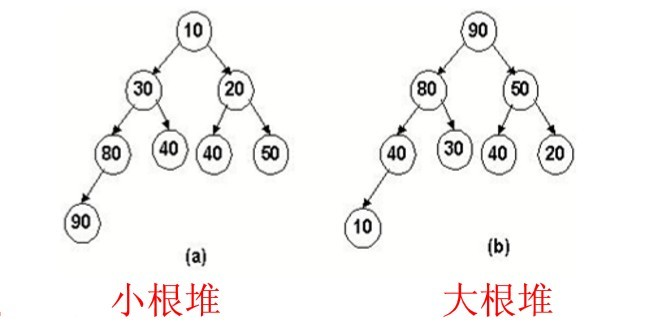
所以这个结构为了考虑到这两种情况，将对比的情况写成抽象方法，由具体大小堆的类去实现这个对比条件，如下：

//定义二叉堆结构
#include <vector>
#include <iostream>
#include <algorithm>  //for swap

template <typename T>
class binary_heap
{
    std::vector<T> data;//这里用系统的vector来存储，比数组要高级一点，而底层实际就是数组，会自动扩容
protected:
  virtual bool compare(T a, T b) = 0;//定义虚方法，具体实现由子类决定
public:
    //插入元素
    void insert(T value) {
        //首先将数据插入从最后插入
        data.push_back(value);
        //当前插入元素在集合中的位置
        int pos = data.size() - ;
        //然后循环不断去找它的父结点进行大写对比
        while(pos > ) {
            //获得父结点在集合中的位置
            int parent = (pos - ) / ;
            //用插入的元素跟父结点进行大小对比，并根据条件将当前元素与父结点进行交换
            if(parent < 0 || !compare(value, data[parent])) {
                //退出循环条件：如果parent如果小于0则代表遍历结束了；如果对比条件不满足【大堆是当前值小于父结点、小堆是当前值大于父结点】
                break;
            }
            //说明需要进行数据交换，采用系统库中的现有函数去做既可
            std::swap(data[pos], data[parent]);
            pos = parent;
        }
    }

    //取出根结点元素
    T root() {
        return data[];
    }

    //删除堆中的根结点
    void delete_root() {
        //TODO
    }

    //判断数组是否为空
    bool empty() {
        return data.empty();
    }

    int size() {
        return data.size();
    }
};

template <typename T>
class max_binary_heap : public binary_heap<T>
{
protected:
  virtual bool compare(T a, T b)
  {
    return a > b;
  }
};

template <typename T>
class min_binary_heap : public binary_heap<T>
{
protected:
  virtual bool compare(T a, T b)
  {
    return a < b;
  }
};

这里为了能看出整个插入的一个排序结果，所以在完成排序之后，将当前元素输出出来：

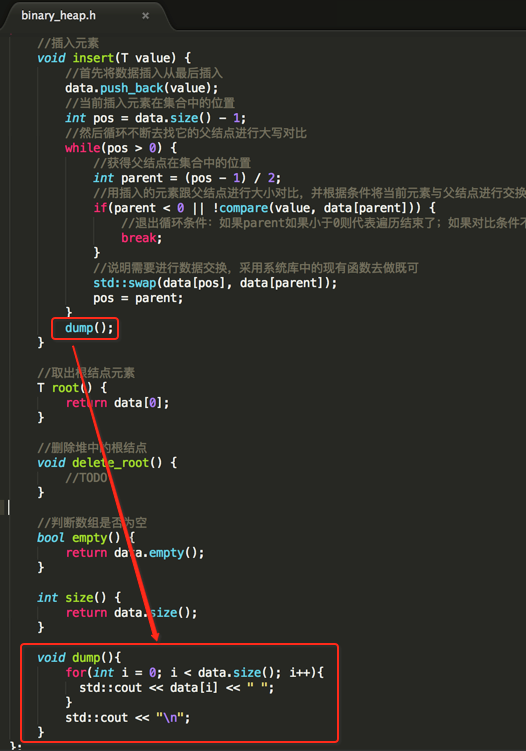
这就是整个的往堆中插入元素的方法，因为比较容易理解这里就不debug啦~

②、delete_root():删除根结点

接着得实现第二个核心方法：从堆中删除根结点，这个在上篇的理论中了将整个删除的过程做了一个详细的阐述，所以这里直接按着其思路来实现它：

接着拿左右子结点跟当前要删除的结点找出最大的数，如图：

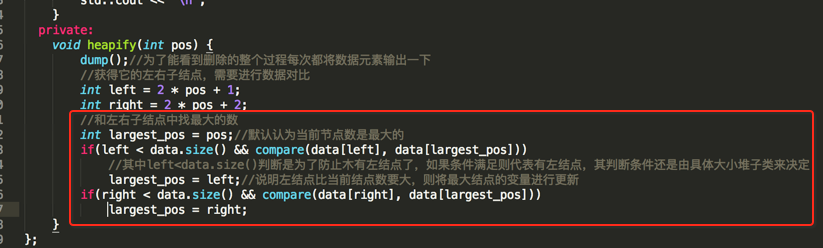
然后拿当前节点跟最大数进行对比，如果当前节点就是最大数则啥都不做递归结束，如果当前节点跟最大数不一样则进行数据交换如下：

至上，整个二叉堆数据结构就已经实现啦，具体如何去使用继续往下看。

完成堆排序：

上面已经定义好了二叉堆的数据结构了，接着来用它完成关键的二叉堆的排序，如下：

具体如何实现呢?有了二叉堆的数据结构了其实非常简单，首先先将待排序的数组元素都插入到堆中【这里用最大堆为例】：

编译运行：

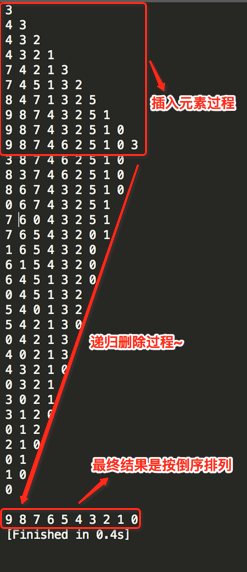
如果想升序排列其实很简单，将最大堆换成最小堆既可，如下：

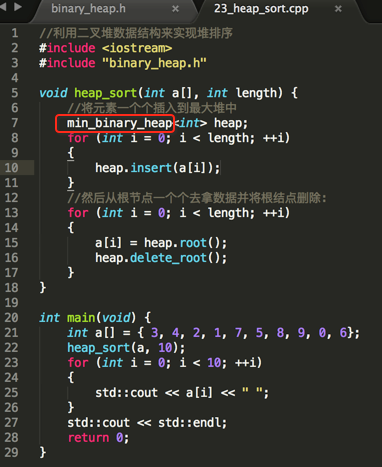
编译运行：

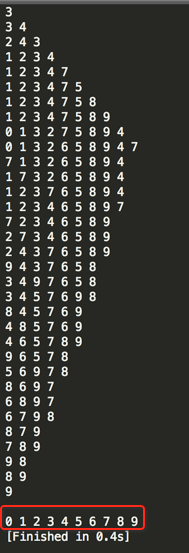
实现拿最大K元素：

堆排序已经实现了，最后就到了这次的主题啦，怎么从大量数据集中拿最大的K个元素呢？

先搭建框架：

思考：是用最小堆还是最大堆去实现？

假如采用最大堆去实现，因为它的根结点永远是最大的，那先将元素都插入到最大堆中，然后拿出k个根结点元素那不就是取出最大的k个元素啦，思路很正点，但是！！！在拿元素之前得先把元素中的所有元素都插入到堆中才行，假如有100万个数，那不这个最大堆的大小就得是100万这个大写，效率貌似不高，所以可以考虑用最小堆试试。

假如采用最小堆，那可以先将前K个元素插入到最小堆中，然后再依次去跟K之外的元素一一跟根结点进行对比，如果比根结点要大则将根结点删除，将这个较大的数插入到最小堆中，也就是！！！永远堆中的数据个数只有K个，而不像最大堆那样堆需要N个元素的大小，这样用最小堆去实现优越感顺间就提升了，所以！这里采用最小堆来实现。

具体如下：

编译运行：

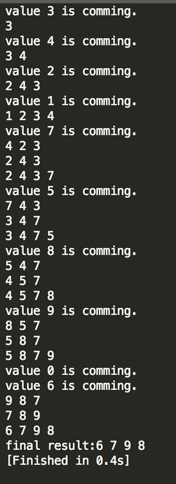
这样就成功找到了最大的K元素啦~

时间复杂度分析：

所以说这里用最小堆实现的时间复杂度是T(n) = O(n * logk)，其中n就是总元数个数，k则是要筛选的K个元素。

但是如果用最大堆实现的话其复杂度就变成了O(n * log n)了，因为循环里面最坏的情况就得进行log n次对比，其中n肯定是比要比k要大得多，所以说用最小堆实现的算法是比较优的。

而如果用最原始通过双层循环的方式来实现：最外层是k次循环，而最里层是n次循环，一个个元素进行大小比较，那这样的时间复杂度就是O(k * n)了，很明显这性能是最差的，虽说实现起来是最容易的。