反向传播神经网络（BP）

实验部分：

①输入、输出矢量及问题的阐述

由题意输入变量取值范围为e={-2,-1,0,1,2}和ec={-2,-1,0,1,2}，则输入矢量有25种情况，分别如下所示：

则由T=int((e+ec)/2) ，采用向下取整，可得输出矢量T为：

该问题可描述为通过训练BP神经网络实现模糊控制规则T=int((e+ec)/2)，并达到网络输出与期望值误差小于0.001。选取较好的BP神经网络参数，包括隐含层节点个数、学习速率等。同时对不同的学习训练算法进行比较，并通过内插方法测试网络。

②给出网络结构

由于有两个输入量，所以输入层采用两个神经元，输出为单值即仅需采用一个神经元。网络采用一个隐含层，假设其神经元节点个数为S1，则网络结构可写为2- S1-1。其中隐含层采用S型激活函数，输出层采用线性激活函数。

针对不同的S1，采用固定误差目标为Err_goal=0.001，固定学习速率0.1，最大迭代次数Max_iteration=10000，采用标准梯度下降训练算法，并通过对网络训练时所需要的循环次数和训练时间的情况观察网络求解效果。

考虑到在不同初始权重和偏差下神经网络性能也可能不同，所以在确定隐含层神经元个数下，选取三次不同初始值，根据平均训练时间和循环次数以及所能达到的精度来确定S1。

表一 隐含层节点寻优

S1	时间/s			循环次数			结果SEE
3	10	10	10	10000	10000	10000	0.0470	0.0326	0.0645
		10			10000			>
8	10	10	10	10000	10000	10000	0.0059	0.0378	0.0013
		10			10000			>
9	7	11	5	7070	10000	5593	0.0010	0.0237	0.0010
		7.6			7553			>
10	10	8	6	9232	7325	6522	0.0010	0.0010	0.0010
		8			7692			=
11	4	2	10	3667	2921	9601	0.0010	0.0010	0.0010
		5.3			5394			=
12	5	11	8	5419	10000	7831	0.0010	0.0039	0.0010
		8			7750			>
13	4	3	6	4840	4054	6762	0.0010	0.0010	0.0010
		4.3			5218.6			=
14	1	6	3	994	6576	3394	0.0010	0.0010	0.0010
		3.3			3654			=

通过上表实验数据，对比可知，当隐含层神经元个数大于10个时结果开始趋于稳定，故选取S1=10，并固定三次训练中最好结果的的初始值，即误差平方和SEE=0.0010，迭代时间为6s，迭代次数为6522次的实验数据。

该网络权重和偏差初始值分别如下：

其中 W^1和 b^1分别为隐含层的权重和偏差，W^2 和 b^2分别为输出层的权重和偏差。

确定好S1后，固定随机初始值开始对学习速率进行寻优

表二 学习速率寻优

	时间/s	循环次数	结果SEE
0.07	11	9225	0.00100
0.08	9	8100	0.00100
0.09	8	7223	0.00100
0.10	7	6522	0.00100
0.11	6	5948	0.00100
0.12	6	5470	0.00100
0.13	6	5066	0.00100
0.14	5	4721	0.00100
0.15	5	4423	0.00100
0.16	4	4163	0.00100
0.17	4	3935	0.00100
0.20	3	3254	0.00099
0.25	12	10000	0.00361

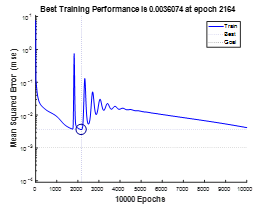
由上图可观察到在学习速率小于0.16时，误差SEE能够平滑快速下降，当 0.17时有毛刺迹象，实验可得0.25时发散，故选择 =0.16。

当采用变学习速率的学习算法，即triangda算法时实验结果如下：

表三 自适应学习速率训练情况

时间/s	循环次数	结果SEE
4	3192	0.0010

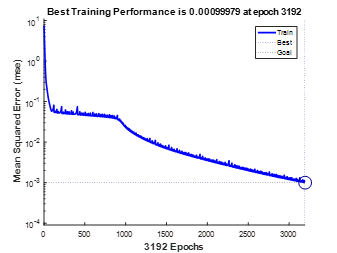
可见自适应算法的收敛速度要快。

③学习方法（包括所采用的改进方法）；

对于不同的权值训练方法，采用S1=10， =0.16，目标精度为0.001，最大迭代次数为10000次，保持参数不变。实验结果如下表所示：

表四 不同学习训练算法对比分析

函数	算法描述	时间/s	迭代次数	结果
traingd	标准梯度下降	4	4163	0.0010
traingdm	附加动量，mc=0.9	11	10000	0.0204
traingda	变学习速率	4	3192	0.0010
traincgf	Fletcher-Powell共轭	2	108	0.00099
traincgp	Powell-Ribiere共轭	<1	103	0.00093
trainscg	Scaled共轭	<1	94	0.00095
trainbfg	BFGs拟牛顿	1	65	0.00081
trainoss	正割拟牛顿	<1	183	0.00099
trainrp	弹性BP算法	<1	184	0.00098
trainlm	Levenberg-Marquardt	<1	29	0.00090

④初始化及必要的参数选取；

初始化必要参数选择（对于标准梯度下降算法）：网络结构2-10-1，即S1=10， =0.16，最大迭代次数10000次，初始化权重和偏差如W^1,b^1,W^2 ,b^2分 所示。

⑤最后的结果，循环次数，训练时间，其中着重讨论：

a)不同隐含层S1时的收敛速度与误差精度的对比分析，详细分析见表一。

b)当S1设置为较好的情况下，在训练过程中取始终不变的学习速率lr值时，对lr值为不同值时的训练时间，包括稳定性进行观察比较，详细分析见表二。

c)当采用自适应值学习速率时，与单一固定的学习速率lr中最好的情况进行对比训练的观察，详细分析见表三。

d)给出结论或体会。

本次实验首先通过对标准梯度下降学习算法的最佳隐含层节点个数和最佳学习速率的寻优，充分了解掌握了BP神经网络的训练方法和结果分析。同时对其他不同的学习算法进行实验分析，其中效果最佳的为Levenberg-Marquardt法，仅需要29次迭代就可以达到目标精度，次优的为BFGs拟牛顿法，需要65次迭代达到目标精度。通过这次实验收获很大。

⑥验证，采用插值法选取多于训练时的输入，对所设计的网络进行验证，给出验证的A与T值。

采用内插值，可知输入变量取值范围为 e=[-2,2]和ec=[-2,2]，选取 30组内插测试集，并通过计算得到期望输出矢量T_test。输入矢量有30种情况，分别如下所示：

通过测试，得到测试结果为：

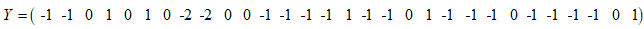
则E=T_test-Y 为：

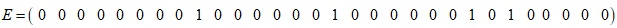
可以看到在30组的测试集中有4组是有误差的，分析原因可知当 的值存在0.5左右的小数时，结果很可能出错，这可能是在得到 和 时采用round()四舍五入运算，而训练样本采用向下取整。

P = [-2 -2 -2 -2 -2 -1 -1 -1 -1 -1 0 0 0 0 0 1 1 1 1 1 2 2 2 2 2;
    -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2];
%T = [-2 -1 -1 -1 0 -1 -1 -1 0 0 -1 -1 0 0 1 -1 0 0 1 1 0 0 1 1 2];
T = [-2 -2 -1 -1 0 -2 -1 -1 0 0 -1 -1 0 0 1 -1 0 0 1 1 0 0 1 1 2];
P_test=[-1.0557   -1.3090    1.2044    1.1025    -0.8188    1.0945   -1.4473   -1.2423   -1.4905   -1.4868   -0.9071 -0.5317   -1.2507   -0.9795   -1.9378    1.8502   -1.9682   -0.5628    0.1633    0.0684   -1.4024   -1.7638    0.8895  0.6688    0.3943   -0.2545   -1.0839    0.0455   -0.6156   0.5526;
    -0.8437   -1.2052   -0.8015    0.7111    0.9226    1.6034    1.1763   -1.8841   -1.4651    1.7410    1.7707 -1.0552    0.1826   -0.7767    0.3500    1.3994    0.5361   -1.5438   -0.3343    1.5445   -0.2613   -0.4759   -1.6195 -0.8144   -1.3926   -1.9493   -0.9453   -1.1397    0.9913   1.4901];
T_test=zeros(1,30);
for i=1:30
T_test(1,i)=round((P_test(1,i)+P_test(2,i))/2);
end
%T_test
% for i=1:25
% plot3(P(1,i),P(2,i),T(i),'ro')
% hold on
% end
w1=[-1.4806   -1.6455
   -1.8388   -1.2325
    2.2000   -0.2448
   -1.6214   -1.5070
   -1.0210    1.9641
   -2.0718   -0.7795
   -0.6118   -2.1274
   -1.6455   -1.4806
    1.9736   -1.0025
   -1.2304   -1.8401];
b1=[4.4272
    3.4434
   -2.4595
    1.4757
    0.4919
   -0.4919
   -1.4757
   -2.4595
    3.4434
   -4.4272];
w2=[0.0109    0.5229    0.2621   -0.8202   -0.8383    0.5545    0.8103   0.0675   -0.7817    0.6516];
b2=-0.3238;
net=newff([-2 2;-2 2],[10,1],{'tansig','purelin'},'trainlm'); %创建两层前向回馈网络
net.trainParam.epochs=10000;  %初始化训练次数
net.trainParam.goal=0.001;
net.trainParam.lr=0.16;
net.trainParam.show = 25;                            %显示循环间隔
%在开始训练之前我们需要知道权重和偏差的随机初始值
% net.IW{1}
% net.b{1}
% net.LW{2}
% net.b{2}
%初始值负值
net.IW{1}=w1;
net.b{1}=b1;
net.LW{2}=w2;
net.b{2}=b2;
[net,tr]=train(net,P,T);                             %训练网络
round(sim(net,P))
T_test
Y=round(sim(net,P_test))                             %计算结果
E=T_test-Y
sumsqr(E)
% net.IW{1}
% net.b{1}
% net.LW{2}
% net.b{2}