Generative Adversarial Network - Python实现

• 算法特征
  
  ①. discriminator区别真假; ②. generator以假乱真

• 算法推导
  
  Part Ⅰ: 熵之相关定义
  
  entropy之定义如下,

  \[\begin{equation*}
  H(p) = -\sum_c p(c)\ln(p(c))
  \end{equation*}
  \]

  entropy衡量自身分布之集中性. 分布越集中, entropy越小.
  
  cross entropy之定义如下,

  \[\begin{equation*}
  \begin{split}
  H(p, q) &= -\sum_c p(c)\ln(q(c)) \\
  &\ge 0
  \end{split}
  \end{equation*}
  \]

  cross entropy衡量不同分布之绝对相似性. 分布越相似, cross entropy越小.
  
  KL divergence之定义如下,

  \[\begin{equation*}
  \begin{split}
  KL(p||q) &= H(p, q) - H(p) \\
  &= -\sum_c p(c)\ln(q(c)) + \sum_c p(c)\ln(p(c)) \\
  &= -\sum_c p(c)\ln\frac{q(c)}{p(c)} \\
  &\ge -\ln\sum_c p(c)\cdot \frac{q(c)}{p(c)} \\
  &= -\ln\sum_c q(c) \\
  &= 0
  \end{split}
  \end{equation*}
  \]

  KL divergence衡量不同分布之相对相似性. 分布越相似, KL divergence越小.
  
  Jensen-Shannon divergence之定义如下,

  \[\begin{equation*}
  JSD(p||q) = \frac{1}{2}KL(p||m) + \frac{1}{2}KL(q||m), \quad\text{where $m=\frac{1}{2}(p+q)$
  and $0 \leq JSD(p||q) \leq \ln 2$}
  \end{equation*}
  \]

  JS divergence下, 若\(p\)与\(q\)完全重合, 则\(JSD(p||q)=0\); 若\(p\)与\(q\)完全不重合, 则\(JSD(p||q)=\ln 2\).
  
  Part Ⅱ: 最大似然估计
  
  Problem:
  
  给定数据分布\(P_{data}(x)\), 以及由\(\theta\)参数化之数据分布\(P_G(x|\theta)\). 现需获得最佳参数\(\theta^*\), 以使分布\(P_G(x|\theta^*)\)尽可能接近分布\(P_{data}(x)\).
  
  Solution:
  
  从分布\(P_{data}(x)\)采样数据集\(\{x^{(1)}, x^{(2)},\cdots,x^{(m)}\}\), 根据最大似然估计,

  \[\begin{equation*}
  \begin{split}
  \theta^* &= \mathop{\arg\max}_\theta\ L(\theta) \\
  &= \mathop{\arg\max}_\theta\ P_G(x^{(1)}, x^{(2)},\cdots,x^{(m)} | \theta) \\
  &= \mathop{\arg\max}_\theta\ \prod_{i=1}^m P_G(x^{(i)}|\theta) \\
  &= \mathop{\arg\max}_\theta\ \ln \prod_{i=1}^m P_G(x^{(i)}|\theta) \\
  &= \mathop{\arg\max}_\theta\ \sum_{i=1}^m \ln P_G(x^{(i)}|\theta) \\
  &\approx \mathop{\arg\max}_\theta\ E_{x\sim P_{data}}[\ln P_G(x|\theta)] \\
  &= \mathop{\arg\max}_\theta\ \int_x P_{data}(x)\ln P_G(x|\theta)\mathrm{d}x \\
  &= \mathop{\arg\max}_\theta\ \int_x P_{data}(x)\ln P_G(x|\theta)\mathrm{d}x - \int_x P_{data}(x)\ln P_{data}(x)\mathrm{d}x \\
  &= \mathop{\arg\min}_\theta\ -\int_x P_{data}(x)\ln P_G(x|\theta)\mathrm{d}x + \int_x P_{data}(x)\ln P_{data}(x)\mathrm{d}x \\
  &= \mathop{\arg\min}_\theta\ KL(P_{data}(x)||P_G(x|\theta))
  \end{split}
  \end{equation*}
  \]

  因此, 不同分布之KL divergence越小, 分布越接近.
  
  Part Ⅲ: GAN之原理
  
  令Generator符号为\(G\), 输入为\(z\)(分布为\(P_{prior}(z)\)), 输出为\(x\)(分布为\(P_G(x)\)). 令Discriminator符号为\(D\), 输入为\(x\), 输出为范围在\((0, 1)\)之scalar(区别真假). 如下图所示,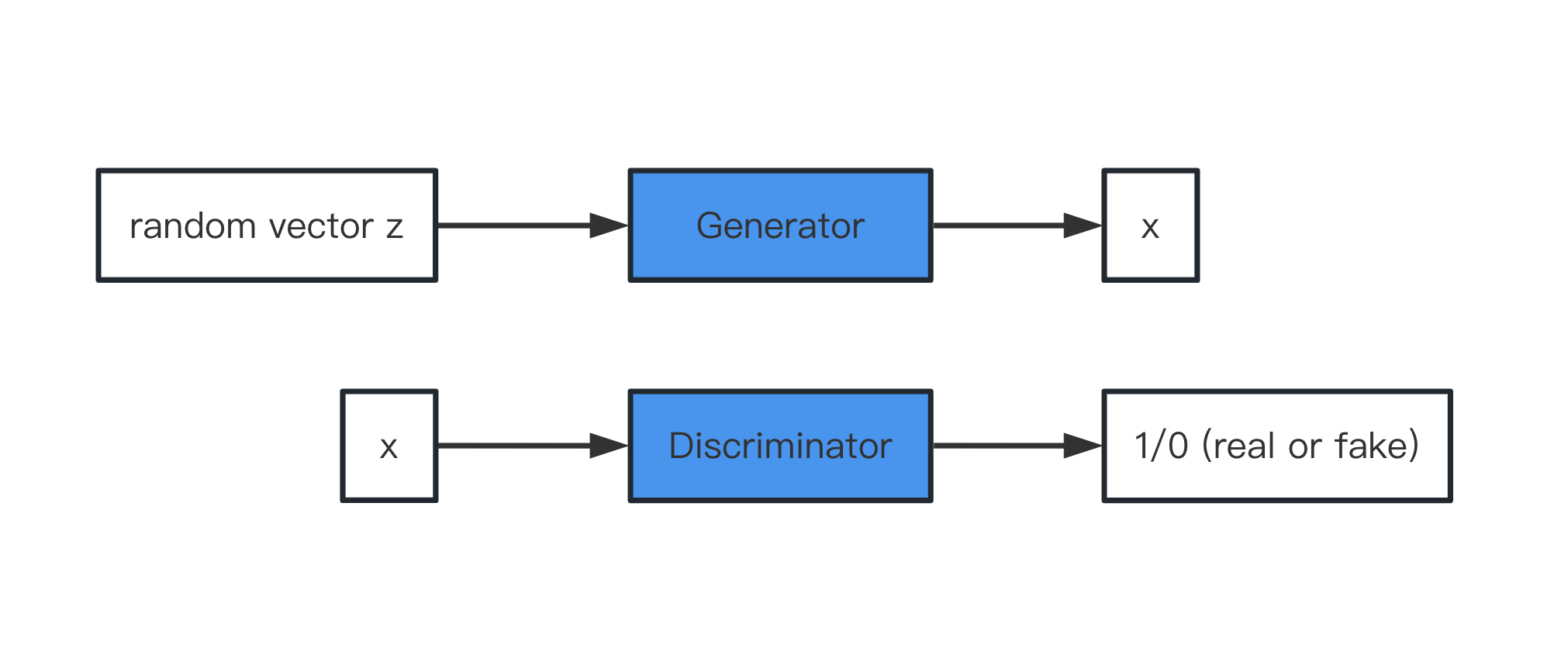

  

  类比交叉熵, 定义如下函数\(V(G, D)\),

  \[\begin{equation*}
  \begin{split}
  V(G, D) &= E_{x\sim P_{data}}[\ln D(x)] + E_{x\sim P_G}[\ln(1 - D(x))] \\
  &= \int_x P_{data}(x)\ln D(x)\mathrm{d}x + \int_x P_G(x)\ln(1-D(x))\mathrm{d}x \\
  &= \int_x [P_{data}(x)\ln D(x) + P_G(x)\ln(1-D(x))]\mathrm{d}x
  \end{split}
  \end{equation*}
  \]

  令,

  \[\begin{align*}
  D^* &= \mathop{\arg\max}_D\ V(G, D) \\
  G^* &= \mathop{\arg\min}_G\max_D\ V(G, D) = \mathop{\arg\min}_G\ V(G, D^*)
  \end{align*}
  \]

  具体地,

  \[\begin{equation*}
  \begin{split}
  D^* &= \mathop{\arg\max}_D\ V(G, D) \\
  &= \mathop{\arg\max}_D\ P_{data}(x)\ln D(x) + P_G(x)\ln(1 - D(x)) \\
  &= \frac{P_{data}(x)}{P_{data}(x) + P_G(x)}
  \end{split}
  \end{equation*}
  \]

  此时有,

  \[\begin{equation*}
  \begin{split}
  V(G, D^*) &= E_{x\sim P_{data}}[\ln\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}] + E_{x\sim P_G}[\ln\frac{P_G(x)}{P_{data}(x) + P_G(x)}] \\
  &= \int_x P_{data}(x)\ln\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}\mathrm{d}x + \int_x P_G(x)\ln\frac{P_G(x)}{P_{data}(x) + P_G(x)}\mathrm{d}x \\
  &= \int_x P_{data}(x)\ln\frac{P_{data}(x)}{(P_{data}(x)+P_G(x))/2}\mathrm{d}x + \int_x P_G(x)\ln\frac{P_G(x)}{(P_{data}(x) + P_G(x))/2}\mathrm{d}x + 2\ln\frac{1}{2} \\
  &= \int_x P_{data}(x)\ln\frac{P_{data}(x)}{(P_{data}(x)+P_G(x))/2}\mathrm{d}x + \int_x P_G(x)\ln\frac{P_G(x)}{(P_{data}(x) + P_G(x))/2}\mathrm{d}x - 2\ln 2 \\
  &= KL(P_{data}(x)||\frac{P_{data}(x)+P_G(x)}{2}) + KL(P_G(x)||\frac{P_{data}(x)+P_G(x)}{2}) - 2\ln 2 \\
  &= 2JSD(P_{data}||P_G(x)) - 2\ln 2
  \end{split}
  \end{equation*}
  \]

  进一步,

  \[\begin{equation*}
  \begin{split}
  G^* &= \mathop{\arg\min}_G\ V(G, D^*) \\
  &= \mathop{\arg\min}_G\ JSD(P_{data}(x)||P_G(x))
  \end{split}
  \end{equation*}
  \]

  因此, \(D^*\)使得函数\(V(G, D)\)具备衡量\(P_{data}(x)\)与\(P_G(x)\)之差异的能力, \(G^*\)则降低此种差异使\(P_G(x)\)趋近于\(P_{data}(x)\).
  
  Part Ⅳ: GAN之实现
  
  实际实现以如下\(\tilde{V}(G, D)\)替代上述\(V(G, D)\)

  \[\begin{equation*}
  \begin{split}
  \tilde{V}(G, D) &= \frac{1}{m}\sum_{i=1}^m \ln D(x^{(i)}) + \frac{1}{m}\sum_{i=1}^m\ln(1-D(\tilde{x}^{(i)})) \\
  &= \frac{1}{m}\sum_{i=1}^m \ln D(x^{(i)}) + \frac{1}{m}\sum_{i=1}^m\ln(1-D(G(z^{(i)})))
  \end{split}
  \end{equation*}
  \]

  其中, \(x^{(i)}\)采样于分布\(P_{data}(x)\), \(z^{(i)}\)采样于分布\(P_{prior}(z)\).
  
  算法流程如下,
  
  Initialize \(\theta_g\) for \(G\) and \(\theta_d\) for \(D\)
  
  for number of training iterations do
  
  \(\quad\) for \(k\) steps do
  
  \(\qquad\) Sample \(m\) noise samples \(\{z^{(1)}, \cdots, z^{(m)}\}\) from the prior \(P_{prior}(z)\)
  
  \(\qquad\) Sample \(m\) examples \(\{x^{(1)}, \cdots, x^{(m)}\}\) from data distribution \(P_{data}(x)\)
  
  \(\qquad\) Update discriminator parameters \(\theta_d\) by ascending its gradient

  \[\begin{equation*}
  \nabla_{\theta_d} \tilde{V}(G, D) = \nabla_{\theta_d} \frac{1}{m}\sum_{i=1}^m [\ln D(x^{(i)}) + \ln(1-D(G(z^{(i)})))]
  \end{equation*}
  \]

  \(\quad\) end for
  
  \(\quad\) Sample another \(m\) noise samples \(\{z^{(1)}, \cdots, z^{(m)}\}\) from the prior \(P_{prior}(z)\)
  
  \(\quad\) Update generator parameter \(\theta_g\) by descending its gradient

  \[\begin{equation*}
  \nabla_{\theta_g} \tilde{V}(G, D) = \nabla_{\theta_g} \frac{1}{m}\sum_{i=1}^m \ln(1-D(G(z^{(i)})))
  \end{equation*}
  \]

  end for

• 代码实现
  
  本文以MNIST数据集为例进行算法实施, 并观察函数\(\tilde{V}(G, D^*)\)取值随训练过程之变化. 具体实现如下,

  code

  import os
  
  import numpy
  import torch
  from torch import nn
  from torch import optim
  from torch.utils import data
  from torchvision import datasets, transforms
  from matplotlib import pyplot as plt
  
  class Generator(nn.Module):
  
      def __init__(self, in_features):
          super(Generator, self).__init__()
          self.__in_features = in_features
          self.__c = 256
          self.__node_num = self.__c * 4 * 4
  
          self.lin1 = nn.Linear(self.__in_features, self.__node_num, dtype=torch.float64)
          self.bn1 = nn.BatchNorm1d(self.__node_num, dtype=torch.float64)
          self.cov2 = nn.Conv2d(self.__c, 256, 1, stride=1, padding=0, dtype=torch.float64)
          self.bn2 = nn.BatchNorm2d(256, dtype=torch.float64)
          self.decov3 = nn.ConvTranspose2d(256, 128, 4, stride=2, padding=1, dtype=torch.float64)
          self.bn3 = nn.BatchNorm2d(128, dtype=torch.float64)
          self.decov4 = nn.ConvTranspose2d(128, 64, 3, stride=2, padding=1, dtype=torch.float64)
          self.bn4 = nn.BatchNorm2d(64, dtype=torch.float64)
          self.decov5 = nn.ConvTranspose2d(64, 1, 2, stride=2, padding=1, dtype=torch.float64)
  
      def forward(self, X):
          X = torch.relu(self.bn1(self.lin1(X)))
          X = X.reshape((-1, self.__c, 4, 4))
          X = torch.relu(self.bn2(self.cov2(X)))
          X = torch.relu(self.bn3(self.decov3(X)))
          X = torch.relu(self.bn4(self.decov4(X)))
          X = torch.tanh(self.decov5(X))
          return X
  
  class Discriminator(nn.Module):
  
      def __init__(self):
          '''
          in: 1 * 28 * 28
          out: scalar
          '''
          super(Discriminator, self).__init__()
  
          self.cov1 = nn.Conv2d(1, 4, 3, stride=1, padding=1, dtype=torch.float64)
          self.bn1 = nn.BatchNorm2d(4, dtype=torch.float64)
          self.cov2 = nn.Conv2d(4, 16, 3, stride=1, padding=1, dtype=torch.float64)
          self.bn2 = nn.BatchNorm2d(16, dtype=torch.float64)
          self.cov3 = nn.Conv2d(16, 64, 3, stride=1, padding=1, dtype=torch.float64)
          self.bn3 = nn.BatchNorm2d(64, dtype=torch.float64)
          self.cov4 = nn.Conv2d(64, 128, 3, stride=1, padding=1, dtype=torch.float64)
          self.bn4 = nn.BatchNorm2d(128, dtype=torch.float64)
          self.lin5 = nn.Linear(128, 1, dtype=torch.float64)
  
      def forward(self, X):
          X = torch.max_pool2d(self.bn1(self.cov1(X)), 2)
          X = torch.max_pool2d(self.bn2(self.cov2(X)), 2)
          X = torch.max_pool2d(self.bn3(self.cov3(X)), 2)
          X = torch.max_pool2d(self.bn4(self.cov4(X)), 2)
          X = self.lin5(torch.squeeze(X))
          return torch.sigmoid(X)
  
  class DatasetX(data.Dataset):
  
      def __init__(self, dataOri):
          self.dataOri = dataOri
  
      def __len__(self):
          return self.dataOri.shape[0]
  
      def __getitem__(self, index):
          return self.dataOri[index]
  
  class DiscLoss(nn.Module):
  
      def __init__(self, geneObj, discObj):
          super(DiscLoss, self).__init__()
          self.G = geneObj
          self.D = discObj
  
      def forward(self, X, Z):
          term1 = torch.log(self.D(X))
          term2 = torch.log(1 - self.D(self.G(Z)))
          term3 = term1 + term2
          loss = torch.mean(term3)
          return loss
  
  class GeneLoss(nn.Module):
  
      def __init__(self, geneObj, discObj):
          super(GeneLoss, self).__init__()
          self.G = geneObj
          self.D = discObj
  
      def forward(self, Z):
          term1 = torch.log(1 - self.D(self.G(Z)))
          loss = torch.mean(term1)
          return loss
  
  def generate_Z(*size):
      Z = torch.rand(size, dtype=torch.float64) - 0.5
      return Z
  
  def train_epoch_disc(loaderX, discLoss, discOpti, maxIter, isPrint=False):
      k = 1
      tag = False
  
      while True:
          for X in loaderX:
              discOpti.zero_grad()
              batch_size = X.shape[0]
              Z = generate_Z(batch_size, 9)
              loss = discLoss(X, Z)
              loss.backward()
              discOpti.step()
              if isPrint:
                  print(f"k = {k}, lossVal = {loss.item()}")
              if k == maxIter:
                  tag = True
                  break
              k += 1
  
          if tag:
              break
      return loss.item()
  
  def train_epoch_gene(batch_size, geneLoss, geneOpti):
      geneOpti.zero_grad()
      Z = generate_Z(batch_size, 9)
      loss = geneLoss(Z)
      loss.backward()
      geneOpti.step()
      return loss.item()
  
  def train_model(loaderX, geneObj, discObj, lr_disc, lr_gene, maxIter, epochs):
      discLoss = DiscLoss(geneObj, discObj)
      discOpti = optim.Adam(discObj.parameters(), lr_disc, maximize=True)
      geneLoss = GeneLoss(geneObj, discObj)
      geneOpti = optim.Adam(geneObj.parameters(), lr_gene)
  
      loss_list = list()
      for epoch in range(epochs):
          lossVal = train_epoch_disc(loaderX, discLoss, discOpti, maxIter)
          train_epoch_gene(batch_size, geneLoss, geneOpti)
          print(f"epoch = {epoch}, lossVal = {lossVal}")
          loss_list.append(lossVal)
  
      return loss_list, geneObj, discObj
  
  def pretrain_model(loaderX, geneObj, discObj, lr_disc, maxIter):
      discLoss = DiscLoss(geneObj, discObj)
      discOpti = optim.Adam(discObj.parameters(), lr_disc, maximize=True)
      train_epoch_disc(loaderX, discLoss, discOpti, maxIter, isPrint=True)
  
  def plot_model(geneObj, Z, filename="plot_model.png"):
      with torch.no_grad():
          X_ = geneObj(Z)
  
      fig, axLst = plt.subplots(3, 3, figsize=(9, 9))
      for idx, ax in enumerate(axLst.flatten()):
          img = X_[idx, 0].numpy()
          ax.imshow(img)
          ax.set(xticks=[], yticks=[])
  
      fig.tight_layout()
      fig.savefig(filename)
      plt.close()
  
  def plot_loss(loss_list, filename="plot_loss.png"):
      fig = plt.figure(figsize=(8, 4))
      ax1 = fig.add_subplot()
      ax1.plot(numpy.arange(len(loss_list)), loss_list, lw=1)
      ax1.set(xlabel="iterCnt", ylabel="$\\tilde{V}$")
      fig.tight_layout()
      fig.savefig(filename)
      plt.close()
  
  def load_model_gene(geneName="./geneObj.pt"):
      if os.path.isfile(geneName):
          print("load geneObj ...")
          geneObj = torch.load(geneName)
      else:
          geneObj = Generator(9)
      return geneObj
  
  def load_model_disc(discName="./discObj.pt"):
      if os.path.isfile(discName):
          print("load discObj ...")
          discObj = torch.load(discName)
      else:
          discObj = Discriminator()
      return discObj
  
  def save_model(model, modelName):
      torch.save(model, modelName)
  
  torch.random.manual_seed(0)
  
  data1 = datasets.MNIST(root="./data", train=True, download=True, \
      transform=transforms.ToTensor()).data.to(torch.float64)
  data2 = datasets.MNIST(root="./data", train=False, download=True, \
      transform=transforms.ToTensor()).data.to(torch.float64)
  dataOri = torch.unsqueeze(torch.cat((data1, data2), dim=0), dim=1)
  dataOri = (dataOri / 255 - 0.5) * 2
  dataX = DatasetX(dataOri)
  batch_size = 256
  loaderX = data.DataLoader(dataX, batch_size=batch_size, shuffle=True)
  
  testZ = generate_Z(9, 9)
  
  geneName = "./geneObj.pt"
  discName = "./discObj.pt"
  geneObj = load_model_gene(geneName)
  discObj = load_model_disc(discName)
  plot_model(geneObj, testZ, "plot_model_beg.png")
  
  loss_list = list()
  for i in range(1000):
      print("*"*20)
      print(f"i = {i}")
      # lr_disc = 0.001
      # maxIter = 10
      # pretrain_model(loaderX, geneObj, discObj, lr_disc, maxIter)
  
      epochs = 10
      lr_disc = 0.0001
      lr_gene = 0.0001
      maxIter = 1
      loss_list_tmp, *_ = train_model(loaderX, geneObj, discObj, lr_disc, lr_gene, maxIter, epochs)
      loss_list.extend(loss_list_tmp)
      if i % 1 == 0:
          plot_model(geneObj, testZ, "plot_model_end.png")
  
  plot_loss(loss_list, "plot_loss.png")
  plot_model(geneObj, testZ, "plot_model_end.png")
  save_model(geneObj, geneName)
  save_model(discObj, discName)
  

• 结果展示
  
  \(\tilde{V}\)取值变化情况如下,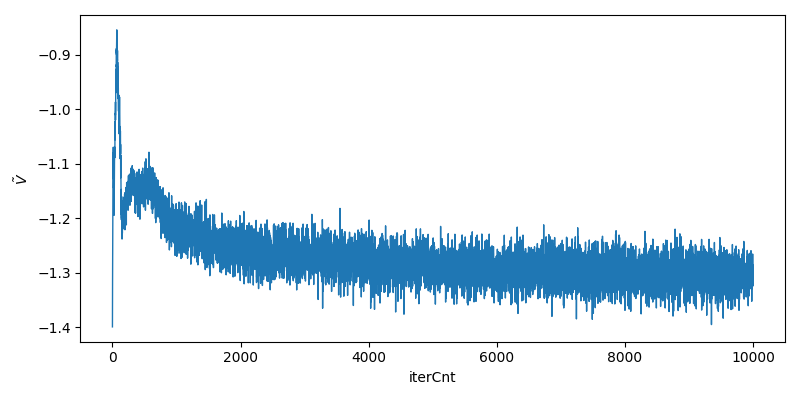

  

  generator训练前生成9张图片如下,

  

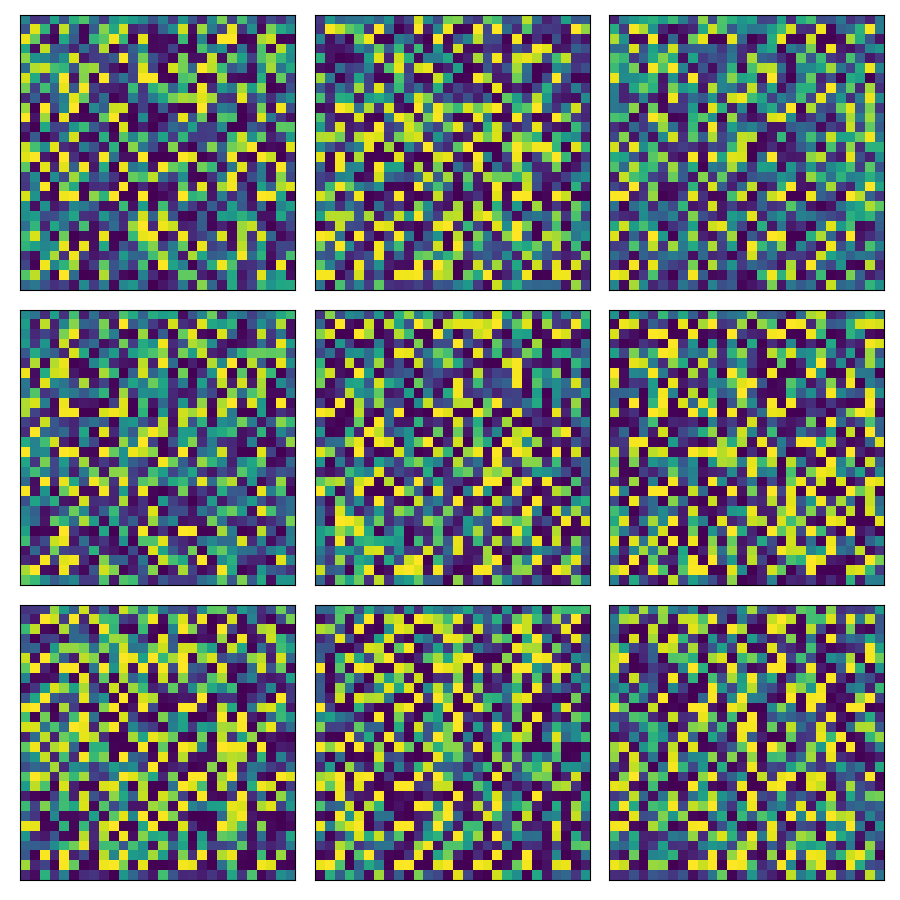
  generator训练后生成9张图片如下,

  

  可以看到, 训练过程中\(\tilde{V}\)逐渐下降, generator生成之图片逐渐"真实".

• 使用建议
  
  ①. torch.float64较torch.float32不容易数值溢出;
  
  ②. 1×1卷积核适合作为全连接层reshape到卷积层之间的过渡层;
  
  ③. 均匀分布随机数适合作为generator之输入.

• 参考文档
  
  ①. 深度学习 - 李宏毅
  
  ②. Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., and Bengio, Y. (2014). Generative adversarial nets. In NIPS’2014.