吴恩达老师机器学习课程chapter08——降维

吴恩达老师机器学习课程chapter08——降维

本文是非计算机专业新手的自学笔记，高手勿喷。

本文仅作速查备忘之用，对应吴恩达(AndrewNg)老师的机器学期课程第十四章。

本章节只有结论，没有任何推演过程，仅作了解入门。

---

目录

• 吴恩达老师机器学习课程chapter08——降维
  • 基本概念
  • 主成分分析法(Principal Component Analysis)
    • 操作
    • 主成分数k的选择
  • 重构

---

基本概念

降维操作可以压缩数据以节约内存，加速算法；还可以为可视化提供便利。

比如，从二维降维至一维：

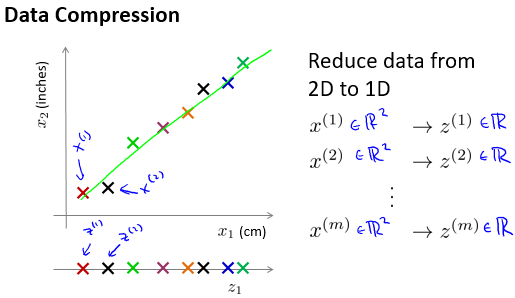
比如，从三维降维至二维：

---

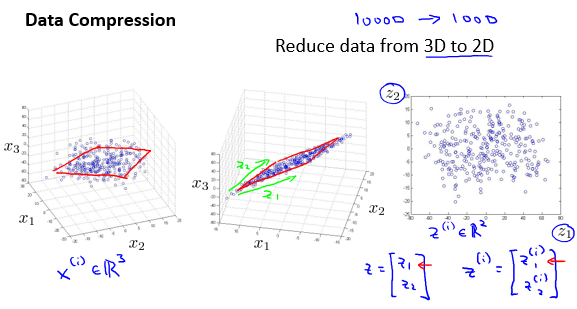
主成分分析法(Principal Component Analysis)

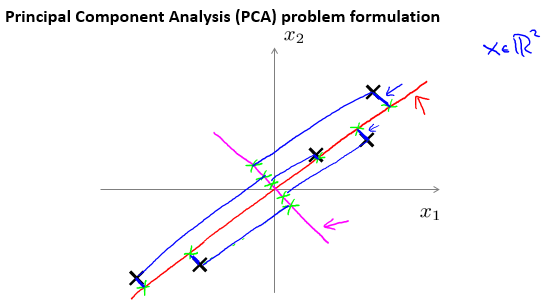
PCA要做的，是寻找到高维空间中，类似于图中红线，而不是图中洋红线，这样的平面。通过这些平面对数据进行降维操作。

样本在这些平面上的投影记作记作\(x^{(i)}_{approx}\)。

要最小化的是平方投影误差。这与回归算法是有区别的。下图中，左侧是回归算法，右侧是PCA算法：

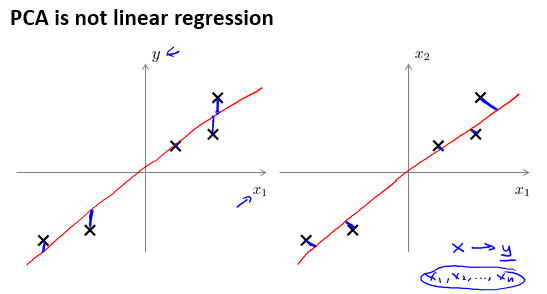
操作

课程中只给出了PCA的操作步骤，没有任何推导：

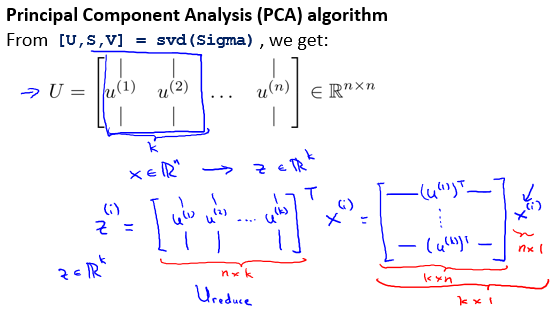
首先，计算矩阵

\[\Sigma=\frac{1}{m} \sum_{i=1}^{n}\left(x^{(i)}\right)\left(x^{(i)}\right)^{T}
\]

之后，进行SVD操作，即奇值分解(Singular Value Decomposition)。这里没有说明具体操作。

得到U矩阵的形状为 n x m，取前 k列，得到新的矩阵——形状为n x k的\(U_{reduce}\)。

$ z^{(i)} = U_{reduce}^T \times x^{(i)}$。完成降维操作。

主成分数k的选择

选择的K值应当使得

\[\frac{ 平均投影误差平方(average\ squared\ projection\ components) }{ 数据总方差(total\ total variation\ in \ the \ deta ) } \le 0.01
\]

也就叫做 “ 保留99％的方差性 ”。95％、90％、85％也是常用的。

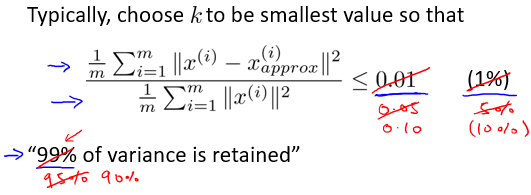
另有计算方法如下：

在奇值分解过程中还会得到n x n的S矩阵，\(s_{ii}\)表示S矩阵对角线元素。

K的选择需要满足：

\[1-\frac{\sum_{i=1}^{k} S_{i i} }{\sum_{i=1}^{n} S_{i i} } \leqslant 0.01
\]

这里0.01与上一种方法的含义是一样的。

---

重构

重构指的是将降维过的数据还原回原本数据的过程。

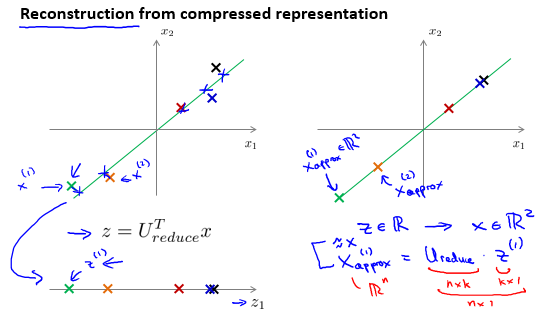
压缩重现计算方法为 $ x_{approx}^{(i)} = U_{reduce}^T \times z^{(i)}$

• PCA并不总是解决过拟合的好办法。
• 先不使用PCA，之后在考察是否需要PCA。