图论分支-Tarjan初步-割点和割边

所谓割点（顶）割边，我们引进一个概念

割点：删掉它之后(删掉所有跟它相连的边)，图必然会分裂成两个或两个以上的子图。
割边(桥)：删掉一条边后，图必然会分裂成两个或两个以上的子图，又称桥。

这样大家就应该能简单理解（怎么可能）割点割边了。

所以我们再来看一个图

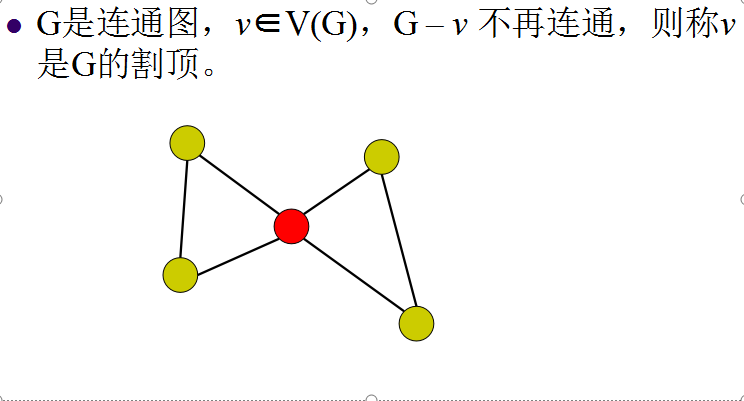
这样大家就能明白了吧（明白是明白了，但是要他干嘛（自动忽略））到后面会明白的。

然后怎么求，这是一个问题，直接想法是搜索，枚举每一个点，然后再去检验是否联通，这样的复杂度应该是O(n2),很显然很不优秀，万一数据是1e5以上不就凉凉了吗。所以我们就可以引进我们的正题了，low-dfn求割点割边。

怎么求？

那么什么是dfn和low呢，简单解释一下，我们的dfn是一个时间戳，也就是访问的时间，而这个就是Tarjan算法的基础（好像忘介绍Tarjan了）而我们的low就是返祖边，也就是通向以前的点的边，所以说，看图。

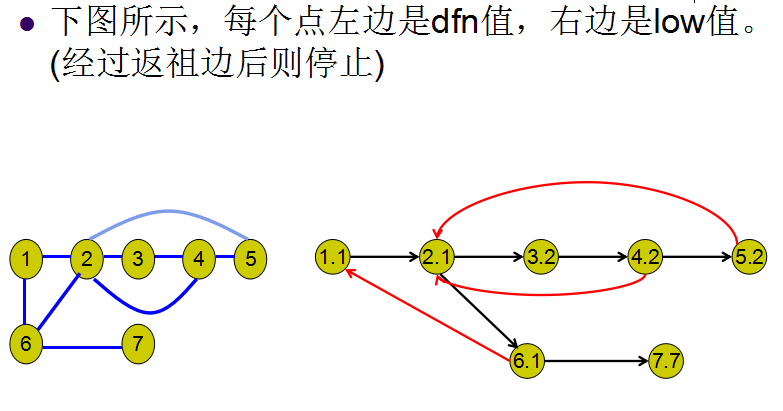
还有一个重要概念也就是，母树继承其子树最小的返祖边，而我们可以观察一下我们的dfn值和low值，再去寻找割点会发现一个重要的事实

每一个割点的dfn一定小于等于其子树的low值，而且如果是root，他的子树大于1他即为割点

这样我们的Code就跃然纸上了

Code

void Tarjan(int x){
    low[x]=dfn[x]=++t;//记录时间戳，当然low值一开始也要与dfn值相同
    for(int i=head[x];i;i=edge[i].next){//链式前向星
        int y=edge[i].to;
        if(!dfn[y]){//如果没有访问过
            Tarjan(y);//搜索查询
            low[x]=min(low[x],low[y]);//母树继承子树的最小low值
            if(low[y]>=dfn[x]){//发现的规律
                flag++;//这个是因为我们的root也有可能是割点，但是它的条件有点苛刻
                if(flag>||x!=root) cut[x]=;//如果子树分支大于1，那么无论他是什么都是割点了
            }
        }else low[x]=min(low[x],dfn[y]);//返祖边，其连接的点继承最小返祖边连接点的dfn值
    }
}

备注应该也是很明白了。

然后我们来看割边，上面已经将概念说的很明白了，删边后，图不联通，然后我们根据一个图来理解割边。

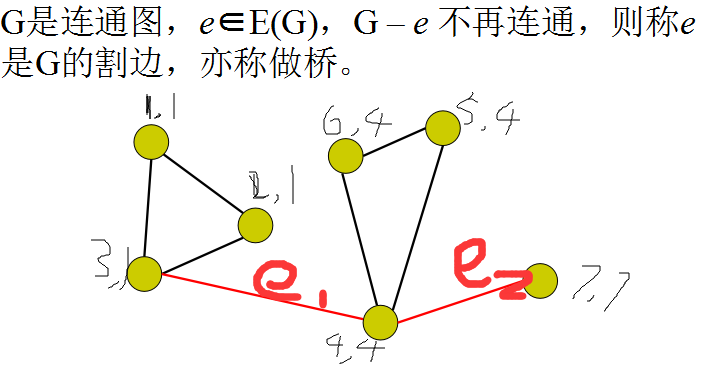
有点丑，左边是dfn，右边是low，红边就是割边，观察一下割边两边两个点的dfn和low值情况，我们会惊喜地发现

母点的dfn值小于（严格小于）子点low值，那么这条边就是割边

好的，我们的代码就出来了

这里引进一道例题

Code

#include<bits/stdc++.h>
using namespace std;
int n,m,head[],cent=,low[],dfn[],t,cnt;
struct node{
    int next,to;
}edge[];
struct prin{
    int u,v;
}ans[];//记录答案 

void add(int u,int v){
    edge[++cent]=(node){head[u],v};head[u]=cent;
}

bool operator <(prin a,prin b){
    if(a.u!=b.u) return a.u<b.u;
    else return a.v<b.v;
}//重载运算符 ，sort要用 

void Tarjan(int x,int fa){//fa定义的是我们走的上一条边
    low[x]=dfn[x]=++t;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            Tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if(low[y]>dfn[x]) {
                ans[++cnt]=x<y?(prin){x,y}:(prin){y,x};//如果结果成立，那么就可以记录这条边的两个点
            } //这里用到了格式转换，prin的定义在上面
        }else if((i^)!=fa){//由于双向建边，需要cent=1，然后用^来验边，或者将fa定义成上一个点
            low[x]=min(low[x],dfn[y]);//
        }
    }
    return ;
}

int main(){
    freopen("danger.in","r",stdin);
    freopen("danger.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=,a,b;i<=m;i++){
        scanf("%d%d",&a,&b);
        if(a==b) continue;//去除自环
        add(a,b),add(b,a);
    }
    for(int i=;i<=n;i++){
        if(!dfn[i]) Tarjan(i,);//不连通时Tarjan，一般都是这样写
    }
    sort(ans+,ans+cnt+);//题目要求
    for(int i=;i<=cnt;i++){
        printf("%d %d\n",ans[i].u,ans[i].v);//输出答案
    }
    return ;
}

这应该就很显然了。

模板讲完了，但还是希望自己的Code要有自己的风格，可以借鉴，但不能照搬。

例题

我们先来看一下割点

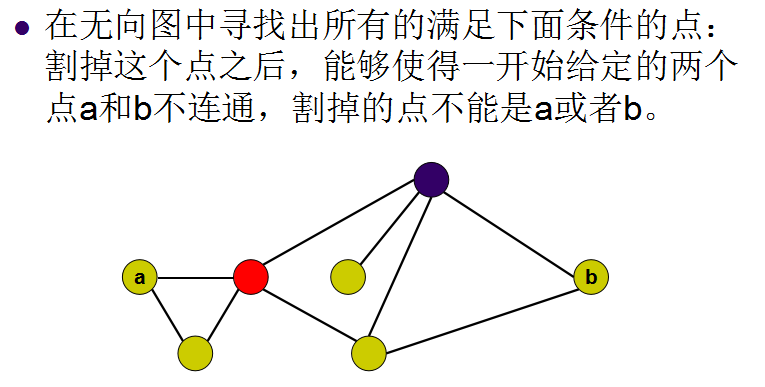
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　——嗅探器

这个显然是要找割点的，那么怎么找呢?

我们的最大问题是有两个点，在去掉割点后，如何检验他们是否在同一个联通块中?

我们首先的思路是暴力枚举割点，然后检验联通，大概能得10%的分，那么我们来想正解

我们可以以a为根，那么就解决了两个点的问题，但是检验呢？

我们可以将Tarjan定义为bool类型即可，然后在Tarjan的过程中，回溯检验值，详情看代码；

Code

#include<bits/stdc++.h>
using namespace std;
int n,a,b,head[],cent,root,fin,low[],dfn[];
int t,cut[];
struct node{
    int next,to;
}edge[];

void add(int u,int v){
    edge[++cent]=(node){head[u],v};head[u]=cent;
}

bool Tarjan(int x){
    low[x]=dfn[x]=++t;
    bool f1=(x==fin);// fin是b点，f1是标记 ，检验有没有b点
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            bool z=Tarjan(y);f1|=z;//回溯标记
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]&&x!=root&&x!=fin&&z){//这里割点一定不是root
                cut[x]=;
            }
        }else{
            low[x]=min(low[x],dfn[y]);
        }
    }
    return f1;//回溯标记
}

int main(){
//    freopen("dfnIn.in","r",stdin);
//    freopen("dfnin.out","w",stdout);
    scanf("%d",&n);
    while(scanf("%d%d",&a,&b)&&(a!=&&b!=)){
        if(a==b) continue;
        add(a,b),add(b,a);
    }
    scanf("%d%d",&root,&fin);
    Tarjan(root);
    for(int i=;i<=n;i++){
        if(cut[i]&&low[fin]>=dfn[i]){//检验
            printf("%d",i);//输出
            return ;
        }
    }
    printf("No solution");
}

这样就让我们对Tarjan的灵活运用有更深理解。

然后来看割边例题

......

其实上面的板子题就是我们的例题（逃）

好了，Tarjan的割点和割边就结束了。

可以自行找些例题，寻找灵感。