UVA1609-Foul Play（构造+递归）

Problem UVA1609-Foul Play

Accept: 101  Submit: 514
Time Limit: 3000 mSec

Problem Description

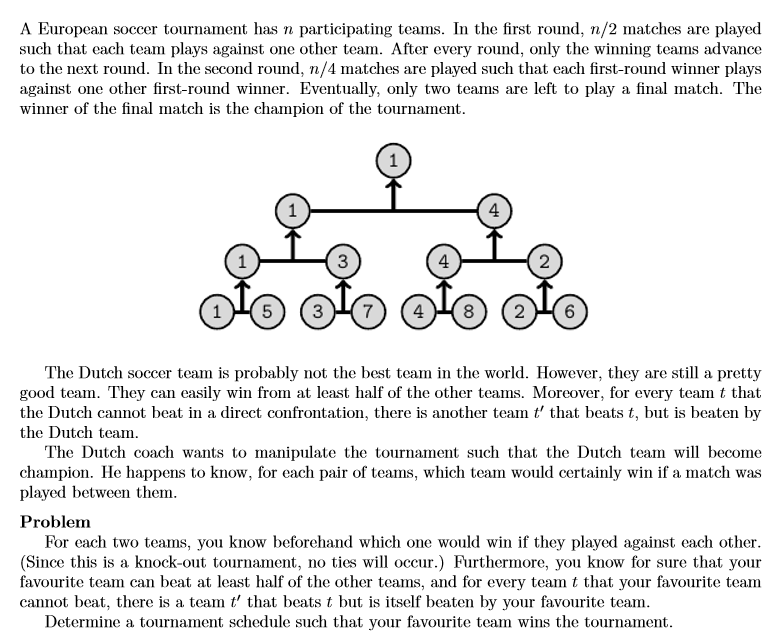
Input

For each test case, the input is as follows:

• One line containing the number of teams n, where n is a power of two and 2 ≤ n ≤ 1024. Teams are numbered from 1 to n, where team 1 is your favourite team.

• n lines, each containing a string of n binary digits. The k-th digit on the j-th line is ‘1’ if team j would certainly win from team k, otherwise it is ‘0’. A team cannot play against itself, therefore the j-th digit on the j-th line is ‘0’. If j ̸= k, the k-th digit on the j-th line is different from the j-th digit on the k-th line.

 Output

For each test case, print n−1 lines of output, specifying a tournament schedule that ensures victory for team 1. The first n/2 lines describe the first round of the tournament. The next n/4 lines describe the second round, if any, etc. The last line describes the final match. Each line contains two integers x and y, indicating that team x plays a match against team y. If there are multiple tournament schedules where team 1 wins, any one of those tournament schedules will be accepted as a correct answer.

 

 Sample Input

4
0110
0011
0000
1010
8
00111010
10101111
00010010
01000101
00110010
10101011
00010000
10101010

 

 Sample Output

1 3
2 4
1 2
1 5
3 7
4 8
2 6
1 3
4 2
1 4

题解：这个题的构造比较难，我是想不到，构造出来之后的递归就相对比较简单了。构造的方式分为四个阶段：

1、把满足条件的队伍A和B配对，其中1打不过A，1能打过B，并且B能打过A.

2、把1和剩下的它能打过的队伍配对.

3、把1打不过的队伍相互配对.

4、把剩下的队伍配对.

能够证明按照这样的策略打过一轮之后，剩下的队伍还满足初始条件，因此可以递归求解。（构造太巧妙orz）

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = ;

 int n;
 char gra[maxn][maxn];
 bool vis[maxn], have_failed[maxn];

 void dfs(int m) {
     if (m == ) return;

     memset(vis, false, sizeof(vis));

     for (int i = ; i <= n; i++) {
         if (have_failed[i] || vis[i]) continue;
         if (gra[][i] == '') {
             for (int j = ; j <= n; j++) {
                 if (have_failed[j] || vis[j]) continue;
                 if (gra[][j] == '' && gra[j][i] == '') {
                     vis[j] = vis[i] = true;
                     have_failed[i] = true;
                     printf("%d %d\n", i, j);
                     break;
                 }
             }
         }
     }

     for (int i = ; i <= n; i++) {
         if (have_failed[i] || vis[i]) continue;
         if (gra[][i] == '') {
             vis[i] = true;
             have_failed[i] = true;
             printf("%d %d\n", , i);
             break;
         }
     }

     int flag = , pre = ;
     for (int i = ; i <= n; i++) {
         if (have_failed[i] || vis[i]) continue;
         if (gra[][i] == '') {
             if (!flag) {
                 flag = ;
                 pre = i;
             }
             else {
                 flag = ;
                 vis[i] = vis[pre] = true;
                 printf("%d %d\n", pre, i);
                 if (gra[pre][i] == '') have_failed[pre] = true;
                 else have_failed[i] = true;
             }
         }
     }

     flag = ;
     for (int i = ; i <= n; i++) {
         if (have_failed[i] || vis[i]) continue;
         if (!flag) {
             flag = ;
             pre = i;
         }
         else {
             flag = ;
             vis[i] = vis[pre] = true;
             printf("%d %d\n", pre, i);
             if (gra[pre][i] == '') have_failed[pre] = true;
             else have_failed[i] = true;
         }
     }

     dfs(m >> );
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     //freopen("output.txt", "w", stdout);
     while (~scanf("%d", &n)) {
         memset(have_failed, false, sizeof(have_failed));
         for (int i = ; i <= n; i++) {
             scanf("%s", gra[i] + );
         }

         dfs(n);
     }
     return ;
 }