Tornado学习笔记(二) 路由/post/get传参

本章我们学习 Tornado 的路由传参等问题

路由

路由的匹配

Tornado的路由匹配采用的是正则匹配

一般情况下不需要多复杂的正则，正则的基本规则如下（站长之家）

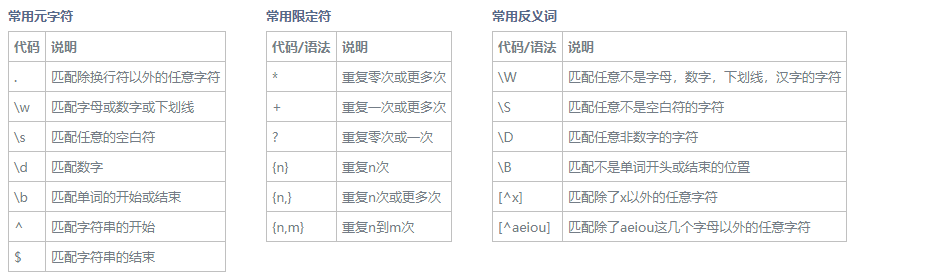
举个例子

(r'/sum/(\d+)', Sum),

该代码指匹配 /sum/  后跟至少一个数字且只有数字的情况

* 需要注意的是网络上传输都是字符串

类 Sum编写

class Sum(tornado.web.RequestHandler):
    # 数字类
    def get(self, sum):
        # 获取数字并返回
        self.write('%s,%s' % (type(sum), sum))

我们访问 http://localhost:8001/sum/12 时

返回正常

我们访问 http://localhost:8001/sum/1a2  http://localhost:8001/sum/a12  http://localhost:8001/sum/12a  http://localhost:8001/sum/a 时，均会报出404错误，证明没有匹配到路由

同理，当我们需要匹配两个参数时

(r'/(\w+)/stuggle/(\d+)', Stugggle),

接收时接收两个参数即可

def get(self, st, ins):
　　pass

post参数

与get一样，post请求会寻找到该视图的 post 方法

我们给视图 Hello 增加一个post

class Hello(tornado.web.RequestHandler):
    # 封装一个类
    def get(self):
        # get请求进入该方法
        self.write('Hello')
    def post(self):
        # post请求
        txt = self.get_argument('txt')
        self.write(txt)

self.get_argument('txt') 指获取post传参中 Key 为 txt 的值，路由无需改动

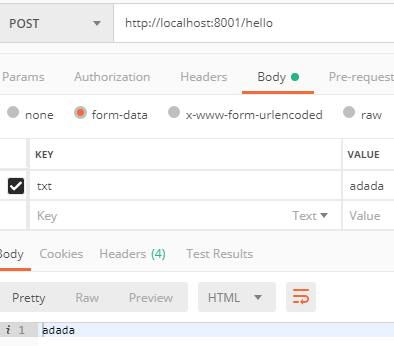
get参数

get获取参数与上面的post没有差别

我们修改get方法来进行测试

    def get(self):
        # get请求进入该方法
        arg = self.get_argument('arg')
        arg1 = self.get_argument('arg1')
        self.write('%s+%s' % (arg,arg1))

但是需要注意的是， get_argument  在获取不到该key时会报错，抛出400错误

get_argument  方法其实可以接收三个参数

get_argument(name,default=_ARG_DEFAULT,strip=True)

第一个参数就是key的值，第二个参数为如果接收不到默认的值，第三个是默认去除前后空格

一般情况下我们第二个参数传 None

    def get(self):
        # get请求进入该方法
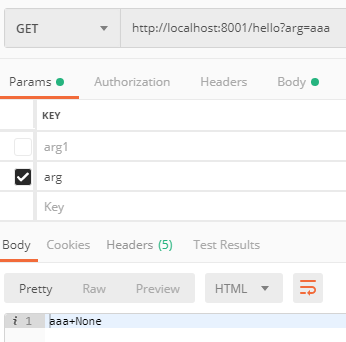
        arg = self.get_argument('arg', None)
        arg1 = self.get_argument('arg1', None)
        self.write('%s+%s' % (arg,arg1))
    def post(self):
        # post请求
        txt = self.get_argument('txt', None)
        self.write(txt)

这样就增加了兼容性