【算法】狄克斯特拉算法（Dijkstra’s algorithm）

狄克斯特拉算法（Dijkstra’s algorithm）

找出最快的路径使用算法——狄克斯特拉算法（Dijkstra’s algorithm）。

使用狄克斯特拉算法

步骤

(1) 找出最便宜的节点，即可在最短时间内前往的节点。

(2) 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。

(3) 重复这个过程，直到对图中的每个节点都这样做了。

(4) 计算最终路径。

术语

权重（weight）：

狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重（weight）。

加权图/非加权图（weighted graph）

带权重的图称为加权图（ weighted graph），不带权重的图称为非加权图（unweighted graph）。

要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。

环

可从一个节点出发，走一圈后又回到这个节点。

无向图意味着两个节点彼此指向对方，其实就是环！

狄克斯特拉算法只适用于有向无环图（directed acyclicgraph，DAG）。

负权边

不能将狄克斯特拉算法用于包含负权边的图

狄克斯特拉算法这样假设：对于处理过的海报节点，没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。

实现

示例：求起点到终点的最短路径

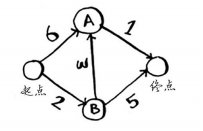
#创建所有节点和路径的散列表
graph={'start': {'a': 6, 'b': 2}, 'a': {'fin': 1}, 'b': {'a': 3, 'fin': 5}, 'fin': {}}  

#创建已知节点花销的散列表
costs={'a': 6, 'b': 2, 'fin': float("inf")}  #float('inf') 表示正无穷                                       

#储存父节点的散列表
parents={'a': 'start', 'b': 'start', 'fin': None}                                       

#存储已访问过节点的列表
processed=[]                                                                            

#定义一个寻找最小花销的函数
def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:      #遍历所有节点
        cost = costs[node]
        if cost < lowest_cost and node not in processed:    #寻找花销最小，且没有访问过的点
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node

node = find_lowest_cost_node(costs)         #找到花销最小的节点
while node is not None:                     #这个while循环在所有节点都被处理过后结束
    cost = costs[node]
    neighbors = graph[node]
    for n in neighbors.keys():              #遍历当前节点的所有邻居
        new_cost = cost + neighbors[n]      #该节点到达该邻居的花销总和
        if costs[n] > new_cost:             #如果经当前节点前往该邻居更近
            costs[n] = new_cost             #更新该邻居的花销
            parents[n] = node               #同时将该邻居的父节点设置为当前节点
    processed.append(node)                  #将当前节点标记为处理过
    node = find_lowest_cost_node(costs)     #找出接下来要处理的节点，并循环

print(parents)

　　

小结

• 广度优先搜索用于在非加权图中查找最短路径。
• 狄克斯特拉算法用于在加权图中查找最短路径。
• 仅当权重为正时狄克斯特拉算法才管用。
• 如果图中包含负权边，请使用贝尔曼福德算法