51Nod 1092 回文字符串（LCS + dp）

51Nod 1092

数据结构暑假作业上出现的一题，学习了一下相关算法之后，找到了oj测试能AC。

1.回文串是一种中心对称的结构，这道题可以转变为求最长回文子序列长度的题目。（子序列：可以不连续）

2.可以得到公式： ans（最少插入字符）= 字符串总长度 - 最长回文子序列长度

3.如何求最长回文子序列的长度呢？ wsx dalao的思路是对区间进行维护（我暂时还写不出来），更一般的做法是动态规划（Dynamic Programming）。

dp 粗略的可以理解为一个状态向另一个状态的转移。一个维度表示一个变量。

仔细想一下的话，很难发现最长回文子序列的长度可以变为求原字符串与其反转字符串最长公共子序列长度（LCS）的题目。

求 LCS 就可以与 dp 联系起来了。

下面列一下状态转移方程：

 /**
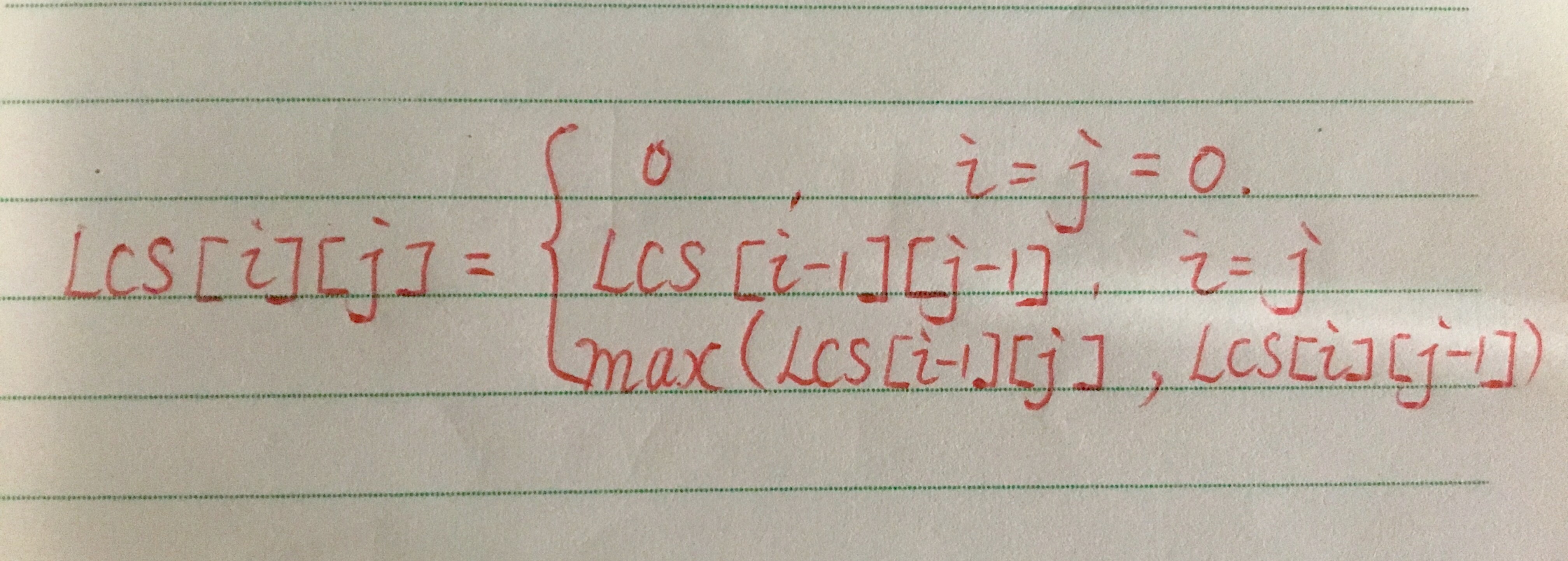
  *  Night gathers, and now my watch begins.
  *  It shall not end until my death.
  *  I shall take no wife, hold no lands, father no children.
  *  I shall wear no crowns and win no glory.
  *  I shall live and die at my post.
  *  I am the sword in the darkness.
  *  I am the watcher on the walls.
  *  I am the fire that burns against the cold,
  *  the light that wakes the sleepers,
  *  the shield that guards the realms of men.
  *  I pledge my life and honor to the Night's Watch,
  *  for this night,
  *  and all the nights to come.
  */

 #include<bits/stdc++.h>
 #define lson i<<2
 #define rson i<<2|1
 #define LS l,mid,lson
 #define RS mid+1,r,rson
 #define mem(a,x) memset(a,x,sizeof(a))
 #define gcd(a,b) __gcd(a,b)
 #define ll long long
 #define ull unsigned long long
 #define lowbit(x) (x&-x)
 #define pb(x) push_back(x)
 #define enld endl
 #define mian main
 #define itn int
 #define prinft printf
 #pragma GCC optimize(2)
 #pragma comment(linker, "/STACK:102400000,102400000")

 const double PI = acos (-1.0);
 const int INF = 0x3f3f3f3f;
 ;
 ;
 ;
 ;

 using namespace std;

 string s;   //题目给的原字符串
 string sr;  //原字符串的翻转字符串
 int dp[MAXN][MAXN]; //dp[i+1][j+1]状态表示为 (s0 ~ si) 和 (s0 ~ sj) 的LCS

 int main() {
     cin >> s;
     mem (dp, );    //dp数组初始化
     sr = s;
     reverse (sr.begin(), sr.end()); //构造翻转串
     ; i <= s.size(); ++i)
         ; j <= sr.size(); ++j)
             ] == sr[j - ])
                 dp[i][j] = dp[i - ][j - ] + ;
             else
                 dp[i][j] = max (dp[i - ][j], dp[i][j - ]);
     cout << s.size() - dp[s.size()][sr.size()] << endl; //ans = s的长度 - LCS(s, sr)
     ;
 }