BFS和DFS算法

昨晚刚昨晚华为笔试题，用到了BFS和DFS，可惜自己学艺不精，忘记了实现原理，现在借用大佬写的内容给自己做个提高

转自：https://www.jianshu.com/p/70952b51f0c8

图是一种灵活的数据结构，一般作为一种模型用来定义对象之间的关系或联系。对象由顶点（V）表示，而对象之间的关系或者关联则通过图的边（E）来表示。
图可以分为有向图和无向图，一般用G=(V,E)来表示图。经常用邻接矩阵或者邻接表来描述一副图。
在图的基本算法中，最初需要接触的就是图的遍历算法，根据访问节点的顺序，可分为广度优先搜索（BFS）和深度优先搜索（DFS）。

---

广度优先搜索（BFS）
广度优先搜索在进一步遍历图中顶点之前，先访问当前顶点的所有邻接结点。
a .首先选择一个顶点作为起始结点，并将其染成灰色，其余结点为白色。
b. 将起始结点放入队列中。
c. 从队列首部选出一个顶点，并找出所有与之邻接的结点，将找到的邻接结点放入队列尾部，将已访问过结点涂成黑色，没访问过的结点是白色。如果顶点的颜色是灰色，表示已经发现并且放入了队列，如果顶点的颜色是白色，表示还没有发现
d. 按照同样的方法处理队列中的下一个结点。
基本就是出队的顶点变成黑色，在队列里的是灰色，还没入队的是白色。
用一副图来表达这个流程如下：

从顶点1开始进行广度优先搜索：

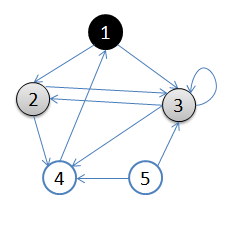
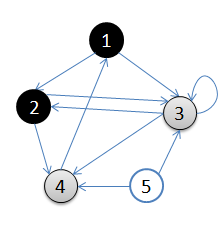
1. 初始状态，从顶点1开始，队列={1}
2. 访问1的邻接顶点，1出队变黑，2,3入队，队列={2,3,}
3. 访问2的邻接结点，2出队，4入队，队列={3,4}
4. 访问3的邻接结点，3出队，队列={4}
5. 访问4的邻接结点，4出队，队列={ 空}
   结点5对于1来说不可达。
   上面的图可以通过如下邻接矩阵表示：

　　

int maze[5][5] = {
    { 0, 1, 1, 0, 0 },
    { 0, 0, 1, 1, 0 },
    { 0, 1, 1, 1, 0 },
    { 1, 0, 0, 0, 0 },
    { 0, 0, 1, 1, 0 }
};

BFS核心代码如下：

#include <iostream>
#include <queue>
#define N 5
using namespace std;
int maze[N][N] = {
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  }
};
int visited[N + ] = { , };
void BFS(int start)
{
    queue<int> Q;
    Q.push(start);
    visited[start] = ;
    while (!Q.empty())
    {
        int front = Q.front();
        cout << front << " ";
        Q.pop();
        for (int i = ; i <= N; i++)
        {
            if (!visited[i] && maze[front - ][i - ] == )
            {
                visited[i] = ;
                Q.push(i);
            }
        }
    }
}
int main()
{
    for (int i = ; i <= N; i++)
    {
        if (visited[i] == )
            continue;
        BFS(i);
    }
    return ;
}

深度优先搜索（DFS）
深度优先搜索在搜索过程中访问某个顶点后，需要递归地访问此顶点的所有未访问过的相邻顶点。
初始条件下所有节点为白色，选择一个作为起始顶点，按照如下步骤遍历：
a. 选择起始顶点涂成灰色，表示还未访问
b. 从该顶点的邻接顶点中选择一个，继续这个过程（即再寻找邻接结点的邻接结点），一直深入下去，直到一个顶点没有邻接结点了，涂黑它，表示访问过了
c. 回溯到这个涂黑顶点的上一层顶点，再找这个上一层顶点的其余邻接结点，继续如上操作，如果所有邻接结点往下都访问过了，就把自己涂黑，再回溯到更上一层。
d. 上一层继续做如上操作，知道所有顶点都访问过。
用图可以更清楚的表达这个过程：

从顶点1开始做深度搜索：

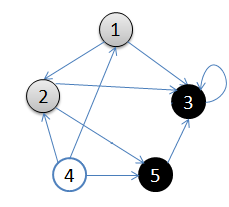
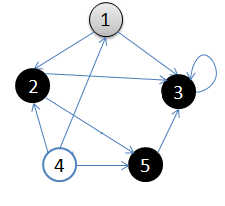
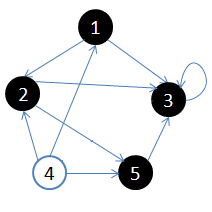
1. 初始状态，从顶点1开始
2. 依次访问过顶点1,2,3后，终止于顶点3
3. 从顶点3回溯到顶点2，继续访问顶点5，并且终止于顶点5
4. 从顶点5回溯到顶点2，并且终止于顶点2
5. 从顶点2回溯到顶点1，并终止于顶点1
6. 从顶点4开始访问，并终止于顶点4

上面的图可以通过如下邻接矩阵表示：

int maze[][] = {
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  }
};

DFS核心代码如下（递归实现）：

#include <iostream>
#define N 5
using namespace std;
int maze[N][N] = {
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  }
};
int visited[N + ] = { , };
void DFS(int start)
{
    visited[start] = ;
    for (int i = ; i <= N; i++)
    {
        if (!visited[i] && maze[start - ][i - ] == )
            DFS(i);
    }
    cout << start << " ";
}
int main()
{
    for (int i = ; i <= N; i++)
    {
        if (visited[i] == )
            continue;
        DFS(i);
    }
    return ;
}

非递归实现如下，借助一个栈：

#include <iostream>
#include <stack>
#define N 5
using namespace std;
int maze[N][N] = {
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  },
    { , , , ,  }
};
int visited[N + ] = { , };
void DFS(int start)
{
    stack<int> s;
    s.push(start);
    visited[start] = ;
    bool is_push = false;
    while (!s.empty())
    {
        is_push = false;
        int v = s.top();
        for (int i = ; i <= N; i++)
        {
            if (maze[v - ][i - ] ==  && !visited[i])
            {
                visited[i] = ;
                s.push(i);
                is_push = true;
                break;
            }
        }
        if (!is_push)
        {
            cout << v << " ";
            s.pop();
        }

    }
}
int main()
{
    for (int i = ; i <= N; i++)
    {
        if (visited[i] == )
            continue;
        DFS(i);
    }
    return ;
}

有的DFS是先访问读取到的结点，等回溯时就不再输出该结点，也是可以的。算法和我上面的区别就是输出点的时机不同，思想还是一样的。DFS在环监测和拓扑排序中都有不错的应用。