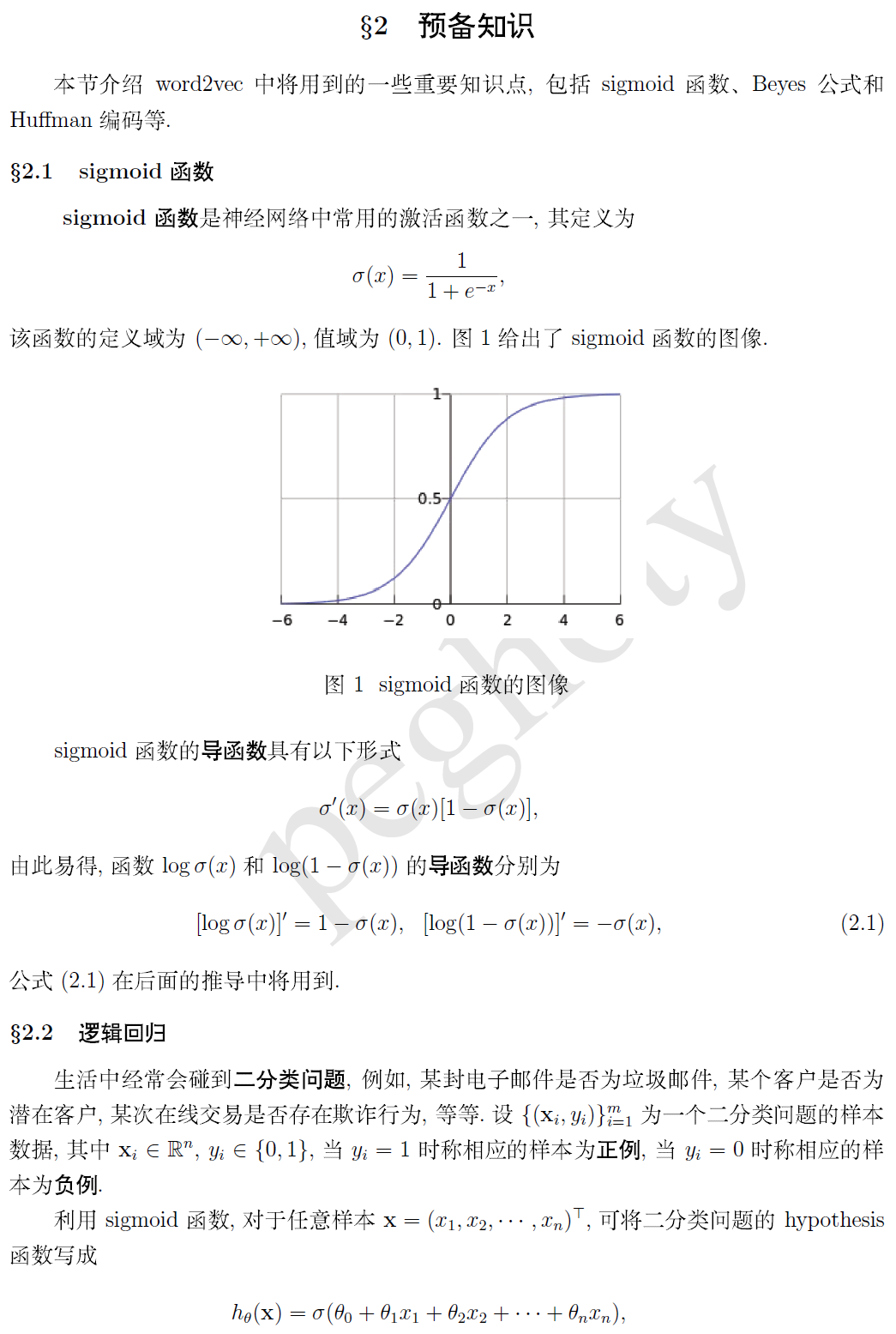
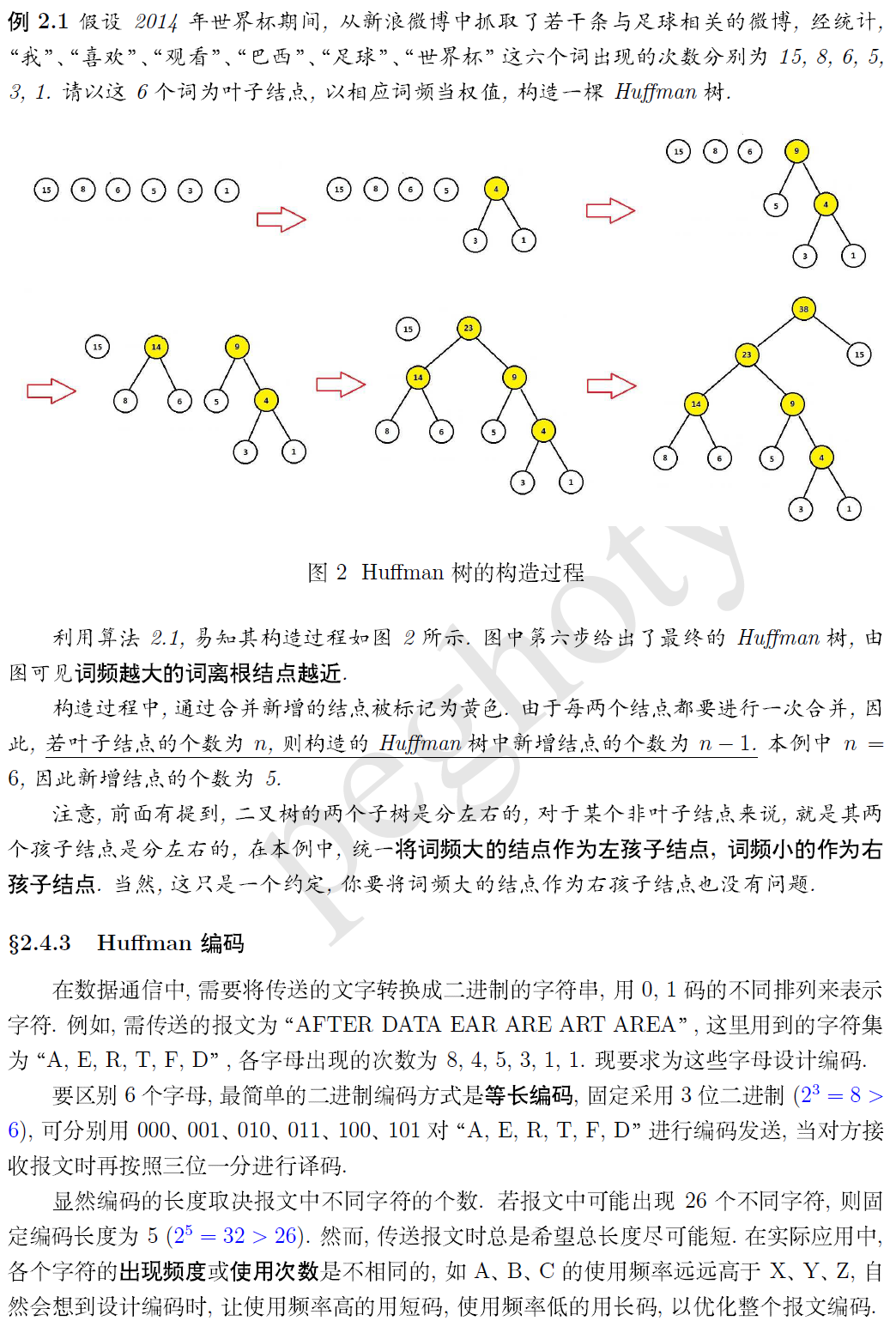
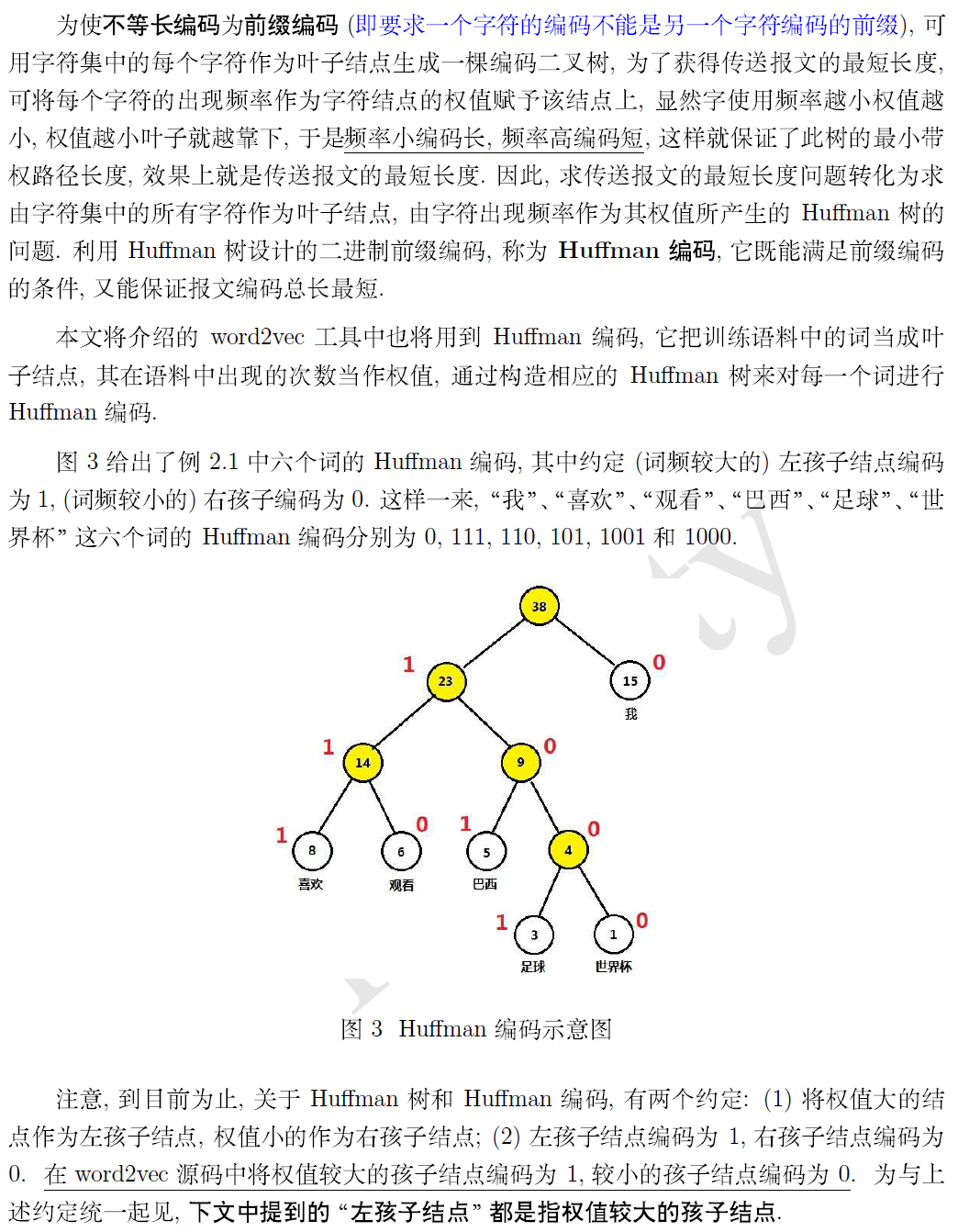
word2vec 中的数学原理二 预备知识 霍夫曼树

主要参考：    word2vec 中的数学原理详解                 自己动手写 word2vec

编码的话，根是不记录在编码中的

这一篇主要讲的就是霍夫曼树（最优二叉树）和编码。  参考   快速画出哈夫曼树 / 霍夫曼树 / 最优树   了解其构成。    哈夫曼树及 python 实现

python 代码 构建霍夫曼树 ，获得霍夫曼编码    简单实现：

#节点类
class Node(object):
    def __init__(self,name=None,value=None):
        self._name=name
        self._value=value
        self._left=None
        self._right=None

#哈夫曼树类
class HuffmanTree(object):

    #根据Huffman树的思想：以叶子节点为基础，反向建立Huffman树
    def __init__(self,char_weights):
        self.a=[Node(part[0],part[1]) for part in char_weights]  #根据输入的字符及其频数生成叶子节点
        while len(self.a)!=1:
            self.a.sort(key=lambda node:node._value,reverse=True)
            c=Node(value=(self.a[-1]._value+self.a[-2]._value))
            c._left=self.a.pop(-1)
            c._right=self.a.pop(-1)
            self.a.append(c)
        self.root=self.a[0]
        self.b=range(10)          #self.b用于保存每个叶子节点的Haffuman编码,range的值只需要不小于树的深度就行
    def show(self):
        pass

    #用递归的思想生成编码
    def pre(self,tree,length):
        node=tree
        if (not node):
            return
        elif node._name:
            print node._name + '的编码为:',
            for i in range(length):
                print self.b[i],
            print '\n'
            return
        self.b[length]=0
        self.pre(node._left,length+1)
        self.b[length]=1
        self.pre(node._right,length+1)
     #生成哈夫曼编码
    def get_code(self):
        self.pre(self.root,0)

if __name__=='__main__':
    #输入的是字符及其频数
    char_weights=[('我',15),('喜欢',8),('观看',6),('巴西',5),('足球',3),('世界杯',1)]
    # char_weights = [('a', 4), ('b', 5), ('c', 8), ('d', 9), ('e', 11), ('f', 13)]
    tree=HuffmanTree(char_weights)
    tree.get_code()

运行结果：

我的编码为:  

世界杯的编码为:     

足球的编码为:     

巴西的编码为:    

观看的编码为:    

喜欢的编码为: