1.softmax初探

1.softmax初探
在机器学习尤其是深度学习中，softmax是个非常常用而且比较重要的函数，尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。
首先我们简单来看看softmax是什么意思。顾名思义，softmax由两个单词组成，其中一个是max。对于max我们都很熟悉，比如有两个变量a,b。如果a>b，则max为a，反之为b。用伪码简单描述一下就是 if a > b return a; else b。
另外一个单词为soft。max存在的一个问题是什么呢？如果将max看成一个分类问题，就是非黑即白，最后的输出是一个确定的变量。更多的时候，我们希望输出的是取到某个分类的概率，或者说，我们希望分值大的那一项被经常取到，而分值较小的那一项也有一定的概率偶尔被取到，所以我们就应用到了soft的概念，即最后的输出是每个分类被取到的概率。

2.softmax的定义
首先给一个图，这个图比较清晰地告诉大家softmax是怎么计算的。

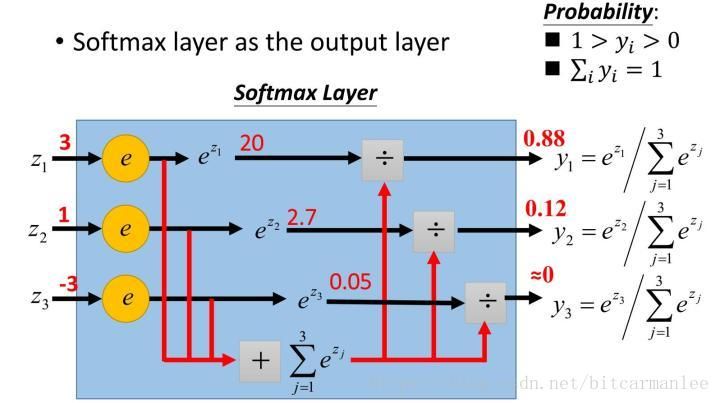
(图片来自网络)

假设有一个数组V，ViVi表示V中的第i个元素，那么这个元素的softmax值为:
Si=ei∑jej
Si=ei∑jej

该元素的softmax值，就是该元素的指数与所有元素指数和的比值。
这个定义可以说很简单，也很直观。那为什么要定义成这个形式呢？原因主要如下。
1.softmax设计的初衷，是希望特征对概率的影响是乘性的。
2.多类分类问题的目标函数常常选为cross-entropy。即L=−∑ktk⋅lnP(y=k)L=−∑ktk⋅lnP(y=k)，其中目标类的tktk为1，其余类的tktk为0。
在神经网络模型中(最简单的logistic regression也可看成没有隐含层的神经网络)，输出层第i个神经元的输入为ai=∑dwidxdai=∑dwidxd。
神经网络是用error back-propagation训练的，这个过程中有一个关键的量是∂L/∂αi∂L/∂αi。后面我们会进行详细推导。

3.softmax求导
前面提到，在多分类问题中，我们经常使用交叉熵作为损失函数
Loss=−∑itilnyi
Loss=−∑itilnyi

其中，titi表示真实值，yiyi表示求出的softmax值。当预测第i个时，可以认为ti=1ti=1。此时损失函数变成了:
Lossi=−lnyi
Lossi=−lnyi

接下来对Loss求导。根据定义：
yi=ei∑jej
yi=ei∑jej

我们已经将数值映射到了0-1之间，并且和为1，则有：
ei∑jej=1−∑j≠iej∑jej
ei∑jej=1−∑j≠iej∑jej
接下来开始求导
∂Lossi∂i=−∂lnyi∂i=∂(−lnei∑jej)∂i=−1ei∑jej⋅∂(ei∑jej)∂i=−∑jejei⋅∂(1−∑j≠iej∑jej)∂i=−∑jejei⋅(−∑j≠iej)⋅∂(1∑jej)∂i=∑jej⋅∑j≠iejei⋅−ei(∑jej)2=∑j≠iej∑jej=−(1−ei∑jej)=yi−1
∂Lossi∂i=−∂lnyi∂i=∂(−lnei∑jej)∂i=−1ei∑jej⋅∂(ei∑jej)∂i=−∑jejei⋅∂(1−∑j≠iej∑jej)∂i=−∑jejei⋅(−∑j≠iej)⋅∂(1∑jej)∂i=∑jej⋅∑j≠iejei⋅−ei(∑jej)2=∑j≠iej∑jej=−(1−ei∑jej)=yi−1
上面的结果表示，我们只需要正想求出yiyi，将结果减1就是反向更新的梯度，导数的计算是不是非常简单！

4.softmax VS k个二元分类器
如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？
这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）
如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？
在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

参考文献：
1.https://www.zhihu.com/question/40403377
2.http://deeplearning.stanford.edu/wiki/index.php/Softmax回归
---------------------
作者：bitcarmanlee
来源：CSDN
原文：https://blog.csdn.net/bitcarmanlee/article/details/82320853
版权声明：本文为博主原创文章，转载请附上博文链接！