Riccati方程迭代法求解
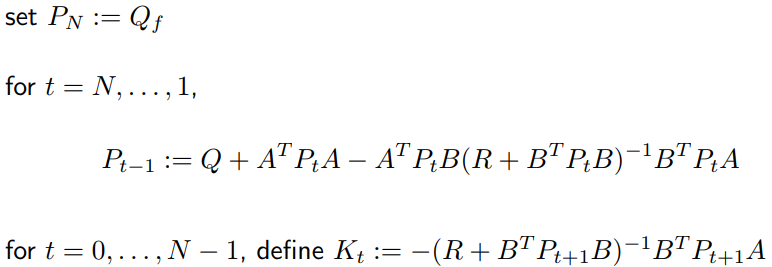
根据上述迭代法求解P,P为Riccati方程的解,然而用LQR需要计算K,再将K算出。
(迭代过程中 ,我们可以将此算法和dlqr函数求解的参数进行对比,当误差小于我们设置的允许误差我们就可以把此算法替换掉dlar函数)
今天我又把离散和连续混在一起了,以后要万分注意,避免bug
Riccati方程迭代法求解的更多相关文章
- Riccati方程(微分方程)
形如:$$\frac{dy}{dx}=P(x)y^{2}+Q(x)y+R(x)$$ 其中P(x).Q(x).R(x)是连续可微函数 或形如 $$\frac{dy}{dx}=ay^{2}+\frac{k ...
- Java实现牛顿迭代法求解平方根、立方根
一.简介 牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法. ...
- 使用“反向传播”迭代法求解y=√10
X=√10,求X,也就是求Y=10 =X2 , X是多少. *重要的思想是,如何转化为可迭代求解的算法问题. *解数学问题,第一时间画图,求导,“直线化”. Y = X2 假如已知Y = 10 ,要求 ...
- LQR要点
新的“A”变成着了这样:Ac = A - KB 基于对象:状态空间形式的系统 能量函数J:也称之为目标函数 Q:半正定矩阵,对角阵(允许对角元素出现0) R:正定矩阵,QR其实就是权重 下面这段话可能 ...
- C语言之基本算法25—牛顿迭代法求方程近似根
//牛顿迭代法! /* ============================================================ 题目:用牛顿迭代法求解3*x*x*x-2*x*x-16 ...
- MATLAB学习笔记(七)——MATLAB解方程与函数极值
(一)线性方程组求解 包含n个未知数,由n个方程构成的线性方程组为: 其矩阵表示形式为: 其中 一.直接求解法 1.左除法 x=A\b; 如果A是奇异的,或者接近奇异的.MATLAB会发出警告信息的. ...
- 牛顿迭代法解指数方程(aX + e^x解 = b )
高中好友突然问我一道这样的问题,似乎是因为他们专业要做一个计算器,其中的一道习题是要求计算器实现这样的功能. 整理一下要求:解aX + e^X = b 方程.解方程精度要求0.01,给定方程只有一解, ...
- PnP 问题方程怎么列?
PnP 问题即 Perspective-n-Point . 有 P3P 方法,使用三个点对就能求解.但是先按照熟悉的方法,写一写.最后写 P3P 方法,P3P 方法还是比较晦涩的,不是无脑方法. 1. ...
- Matlab-11:Gausssidel迭代法工具箱
算法推导: function [u,n]=GaussSeid(A,b,u0,eps,M) %GaussSeid.m为用高斯-塞德尔迭代法求解线性方程组 %A为线性方程组的系数矩阵 %b为线性方程组的常 ...
随机推荐
- 50个SQL语句(MySQL版) 问题二十
--------------------------表结构-------------------------- student(StuId,StuName,StuAge,StuSex) 学生表 tea ...
- CSS3新增伪类有那些?
p:first-of-type 选择属于其父元素的首个元素 p:last-of-type 选择属于其父元素的最后元素 p:only-of-type 选择属于其父元素唯一的元素 p:only-child ...
- @Transactional 注解失效场景
@Transactional可以用在接口.类.类方法上. 作用于类:当把@Transactional注解放在类上时,表示该类的所有public方法都配置了该事物注解. 作用于方法:表示该方法配置了事物 ...
- 分布式事务专题笔记(二)分布式事务解决方案之 2PC(两阶段提交)
个人博客网:https://wushaopei.github.io/ (你想要这里多有) 前面已经了解了分布式事务的基础理论,以理论为基础,针对不同的分布式场景业界常见的解决方案有2PC.TCC ...
- Java实现 洛谷 P1028 数的计算
import java.util.Scanner; import java.util.Arrays; public class Main { private static Scanner cin; p ...
- java实现第四届蓝桥杯带分数
带分数 题目描述 100 可以表示为带分数的形式:100 = 3 + 69258 / 714 还可以表示为:100 = 82 + 3546 / 197 注意特征:带分数中,数字1~9分别出现且只出现一 ...
- portapack h1 买回来刷hackrf与使用说明
买回来很兴奋,别着急,先不用装扩展板!刷好支持扩展屏的固件,才能用!-------------------------------------hackrf连接电脑windows系统win7/win10 ...
- 算法讲堂二:组合数学 & 概率期望DP
组合数学 1. 排列组合 1. 加法原理 完成一列事的方法有 n 类,其中第 i 类方法包括\(a_i\)种不同的方法,且这些方法互不重合,则完成这件事共有 \(a_1 + a_2 + \cdots ...
- 解析HOT原理
2020-06-09 19:31:01 一.疑问 前段时间:QQ群里有人对“这个表(0,4)这行数据我做了update操作,查看索引的page数据,看到索引一直指向(0,4),用ctid='(0,4) ...
- 【Jmeter】分布式压测环境配置
注意:以下四点都必须一致 1.jmeter版本 2.内置插件 3.jdk版本1.8以上 4.同属一个局域网 助攻机设置 本机助攻机Linux系统,首先需要安装JDK并配置环境 JDk基本安装及配置环境 ...
