2020-07-28：已知sqrt (2)约等于 1.414，要求不用数学库，求sqrt (2)精确到小数点后 10 位。

福哥答案2020-07-28：

1.二分法。
2.手算法。
3.牛顿迭代法。基础是泰勒级数展开法。
4.泰勒级数法。
5.平方根倒数速算法，卡马克反转。基础是牛顿迭代法。

golang代码如下：

package test28_sqrt

import (
    "fmt"
    "math"
    "strconv"
    "testing"
)

const (
    EPSINON = 0.0000000001
)

//go test -v -test.run TestSqrt
func TestSqrt(t *testing.T) {
    f := 2.0
    fmt.Printf("%v 系统自带\r\n", strconv.FormatFloat(math.Sqrt(f), 'f', -1, 64))
    fmt.Println("--------------------------------------------")
    fmt.Printf("%v 二分法结果\r\n", strconv.FormatFloat(sqrtDichotomy(f), 'f', -1, 64))
    fmt.Printf("%v 手算法\r\n", strconv.FormatFloat(sqrtHand(f), 'f', -1, 64))
    fmt.Printf("%v 牛顿迭代法结果\r\n", strconv.FormatFloat(sqrtNewton(f), 'f', -1, 64))
    fmt.Printf("%v 泰勒级数法结果\r\n", strconv.FormatFloat(sqrtTaylor(f), 'f', -1, 64))
    fmt.Printf("%v 64位平方根倒数速算法结果1，精度上不符合\r\n", strconv.FormatFloat(sqrtRootFloat64(f), 'f', -1, 64))
    fmt.Printf("%v 64位平方根倒数速算法结果2，精度上不符合\r\n", strconv.FormatFloat(float64(InvSqrt64(f)), 'f', -1, 64))
    fmt.Println("--------------------------------------------")
    f2 := float32(f)
    fmt.Printf("%v 32位平方根倒数速算法结果1，精度上不符合\r\n", strconv.FormatFloat(float64(sqrtRootFloat32(f2)), 'f', -1, 64))
    fmt.Printf("%v 32位平方根倒数速算法结果2，精度上不符合\r\n", strconv.FormatFloat(float64(InvSqrt32(f2)), 'f', -1, 64))
}

//二分法
func sqrtDichotomy(f float64) float64 {
    left := 0.0
    right := f
    if f < 1 {
        right = 1
    }

    mid := f / 2   //不写0.0的原因是for循环可能进不了，0值明显不对
    mid_mid := 0.0 //mid*mid的值
    for right-left > EPSINON {
        mid = (left + right) / 2.0
        mid_mid = mid * mid
        if mid_mid > f {
            right = mid
        } else if mid_mid < f {
            left = mid
        } else {
            return mid
        }
    }

    return mid
}

//牛顿迭代法.基础是泰勒级数展开法
func sqrtNewton(f float64) float64 {
    z := 1.0
    for math.Abs(z*z-f) > EPSINON {
        z = (z + f/z) / 2
    }
    return z
}

//手算法
func sqrtHand(f float64) float64 {
    i := int64(f)
    ret := 0.0      //返回值
    rettemp := 0.0  //大的返回值
    retsinge := 0.5 //单个值

    //获取左边第一个1，retsingle就是左边的第一个1的值
    for i > 0 {
        i >>= 2
        retsinge *= 2
    }

    rettemp_rettemp := 0.0
    for {
        rettemp = ret + retsinge
        rettemp_rettemp = rettemp * rettemp
        if math.Abs(rettemp_rettemp-f) > EPSINON {
            if rettemp_rettemp > f {

            } else {
                ret = rettemp
            }
            retsinge /= 2
        } else {
            return rettemp
        }
    }
}

//泰勒级数展开法
func sqrtTaylor(f float64) float64 {
    correction := 1.0
    for f >= 2.0 {
        f /= 4
        correction *= 2
    }
    return taylortemp(f) * correction
}
func taylortemp(x float64) float64 { //计算[0,2)范围内数的平方根
    var sum, coffe, factorial, xpower, term float64
    var i int
    sum = 0
    coffe = 1
    factorial = 1
    xpower = 1
    term = 1
    i = 0
    for math.Abs(term) > EPSINON {
        sum += term
        coffe *= 0.5 - float64(i)
        factorial *= float64(i) + 1
        xpower *= x - 1
        term = coffe * xpower / factorial
        i++
    }
    return sum
}

//32位平方根倒数速算法1.卡马克反转。基础是牛顿迭代法。
func sqrtRootFloat32(number float32) float32 {
    var i uint32
    var x, y float32
    f := float32(1.5)
    x = float32(number * 0.5)
    y = number
    i = math.Float32bits(y)     //内存不变，浮点型转换成整型
    i = 0x5f3759df - (i >> 1)   //0x5f3759df,注意这一行，另一个数字是0x5f375a86
    y = math.Float32frombits(i) //内存不变，浮点型转换成整型
    y = y * (f - (x * y * y))
    y = y * (f - (x * y * y))
    return number * y
}

//32位平方根倒数速算法2
func InvSqrt32(x1 float32) float32 {
    x := x1
    xhalf := float32(0.5) * x
    i := math.Float32bits(xhalf)       // get bits for floating VALUE
    i = 0x5f375a86 - (i >> 1)          // gives initial guess y0
    x = math.Float32frombits(i)        // convert bits BACK to float
    x = x * (float32(1.5) - xhalf*x*x) // Newton step, repeating increases accuracy
    x = x * (float32(1.5) - xhalf*x*x) // Newton step, repeating increases accuracy
    x = x * (float32(1.5) - xhalf*x*x) // Newton step, repeating increases accuracy
    return 1 / x
}

//64位平方根倒数速算法1.卡马克反转。基础是牛顿迭代法。
func sqrtRootFloat64(number float64) float64 {
    var i uint64
    var x, y float64
    f := 1.5
    x = number * 0.5
    y = number
    i = math.Float64bits(y)           //内存不变，浮点型转换成整型
    i = 0x5fe6ec85e7de30da - (i >> 1) //0x5f3759df,注意这一行，另一个数字是0x5f375a86
    y = math.Float64frombits(i)       //内存不变，浮点型转换成整型
    y = y * (f - (x * y * y))
    y = y * (f - (x * y * y))
    return number * y
}

//64位平方根倒数速算法2
func InvSqrt64(x1 float64) float64 {
    x := x1
    xhalf := 0.5 * x
    i := math.Float64bits(xhalf)      // get bits for floating VALUE
    i = 0x5fe6ec85e7de30da - (i >> 1) // gives initial guess y0
    x = math.Float64frombits(i)       // convert bits BACK to float
    x = x * (1.5 - xhalf*x*x)         // Newton step, repeating increases accuracy
    x = x * (1.5 - xhalf*x*x)         // Newton step, repeating increases accuracy
    x = x * (1.5 - xhalf*x*x)         // Newton step, repeating increases accuracy
    return 1 / x
}

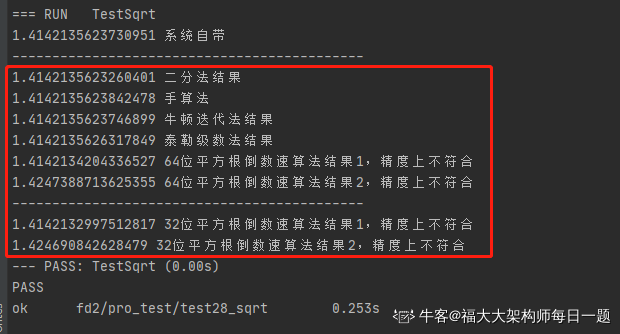
　　敲命令 go test -v -test.run TestSqrt后，结果如下：