机器学习(四)：通俗理解支持向量机SVM及代码实践

上一篇文章我们介绍了使用逻辑回归来处理分类问题，本文我们讲一个更强大的分类模型。本文依旧侧重代码实践，你会发现我们解决问题的手段越来越丰富，问题处理起来越来越简单。

支持向量机(Support Vector Machine, SVM)是最受欢迎的机器学习模型之一。它特别适合处理中小型复杂数据集的分类任务。

一、什么是支持向量机

SMV在众多实例中寻找一个最优的决策边界，这个边界上的实例叫做支持向量，它们“支持”（支撑）分离开超平面，所以它叫支持向量机。

那么我们如何保证我们得到的决策边界是最优的呢？

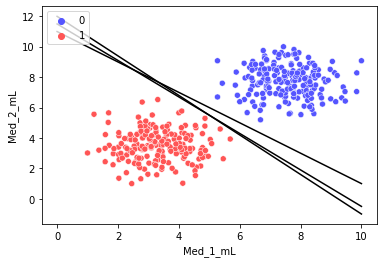
如上图，三条黑色直线都可以完美分割数据集。由此可知，我们仅用单一直线可以得到无数个解。那么，其中怎样的直线是最优的呢？

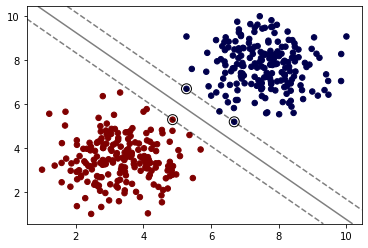
如上图，我们计算直线到分割实例的距离，使得我们的直线与数据集的距离尽可能的远，那么我们就可以得到唯一的解。最大化上图虚线之间的距离就是我们的目标。而上图中重点圈出的实例就叫做支持向量。

这就是支持向量机。

二、从代码中映射理论

2.1 导入数据集

添加引用：

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

导入数据集（大家不用在意这个域名）：

df = pd.read_csv('https://blog.caiyongji.com/assets/mouse_viral_study.csv')
df.head()

	Med_1_mL	Med_2_mL	Virus Present
0	6.50823	8.58253	0
1	4.12612	3.07346	1
2	6.42787	6.36976	0
3	3.67295	4.90522	1
4	1.58032	2.44056	1

该数据集模拟了一项医学研究，对感染病毒的小白鼠使用不同剂量的两种药物，观察两周后小白鼠是否感染病毒。

• 特征： 1. 药物Med_1_mL 药物Med_2_mL
• 标签：是否感染病毒（1感染/0不感染）

2.2 观察数据

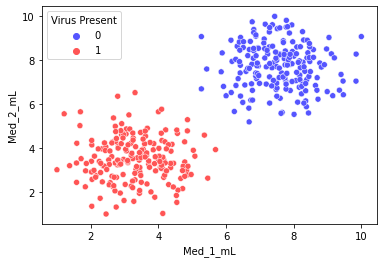
sns.scatterplot(x='Med_1_mL',y='Med_2_mL',hue='Virus Present',data=df)

我们用seaborn绘制两种药物在不同剂量特征对应感染结果的散点图。

sns.pairplot(df,hue='Virus Present')

我们通过pairplot方法绘制特征两两之间的对应关系。

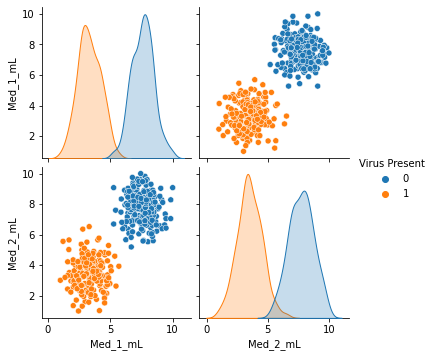
我们可以做出大概的判断，当加大药物剂量可使小白鼠避免被感染。

2.3 使用SVM训练数据集

#SVC: Supprt Vector Classifier支持向量分类器
from sklearn.svm import SVC

#准备数据
y = df['Virus Present']
X = df.drop('Virus Present',axis=1) 

#定义模型
model = SVC(kernel='linear', C=1000)

#训练模型
model.fit(X, y)

# 绘制图像
# 定义绘制SVM边界方法
def plot_svm_boundary(model,X,y):

    X = X.values
    y = y.values

    # Scatter Plot
    plt.scatter(X[:, 0], X[:, 1], c=y, s=30,cmap='coolwarm')

    # plot the decision function
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # create grid to evaluate model
    xx = np.linspace(xlim[0], xlim[1], 30)
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = model.decision_function(xy).reshape(XX.shape)

    # plot decision boundary and margins
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])
    # plot support vectors
    ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
               linewidth=1, facecolors='none', edgecolors='k')
    plt.show()
plot_svm_boundary(model,X,y)

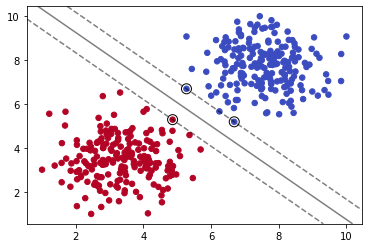
我们导入sklearn下的SVC(Supprt Vector Classifier)分类器，它是SVM的一种实现。

2.4 SVC参数C

SVC方法参数C代表L2正则化参数，正则化的强度与C的值城反比，即C值越大正则化强度越弱，其必须严格为正。

model = SVC(kernel='linear', C=0.05)
model.fit(X, y)
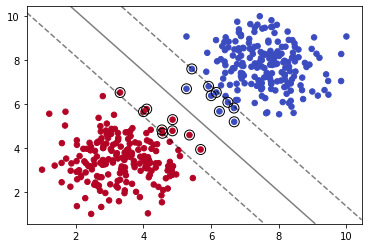
plot_svm_boundary(model,X,y)

我们减少C的值，可以看到模型拟合数据的程度减弱。

2.5 核技巧

SVC方法的kernel参数可取值{'linear', 'poly', 'rbf', 'sigmoid', 'precomputed'}。像前文中所使用的那样，我们可以使kernel='linear'进行线性分类。那么如果我们像进行非线性分类呢？

2.5.1 多项式内核

多项式内核kernel='poly'的原理简单来说就是，用单一特征生成多特征来拟合曲线。比如我们拓展X到y的对应关系如下：

	X	X^2	X^3	y
0	6.50823	6.50823**2	6.50823**3	0
1	4.12612	4.12612**2	4.12612**3	1
2	6.42787	6.42787**2	6.42787**3	0
3	3.67295	3.67295**2	3.67295**3	1
4	1.58032	1.58032**2	1.58032**3	1

这样我们就可以用曲线来拟合数据集。

model = SVC(kernel='poly', C=0.05,degree=5)
model.fit(X, y)
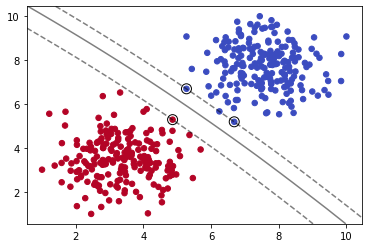
plot_svm_boundary(model,X,y)

我们使用多项式内核，并通过degree=5设置多项式的最高次数为5。我们可以看出分割出现了一定的弧度。

2.5.2 高斯RBF内核

SVC方法默认内核为高斯RBF，即Radial Basis Function（径向基函数）。这时我们需要引入gamma参数来控制钟形函数的形状。增加gamma值会使钟形曲线变得更窄，因此每个实例影响的范围变小，决策边界更不规则。减小gamma值会使钟形曲线变得更宽，因此每个实例的影响范围变大，决策边界更平坦。

model = SVC(kernel='rbf', C=1,gamma=0.01)
model.fit(X, y)
plot_svm_boundary(model,X,y)

2.6 调参技巧：网格搜索

from sklearn.model_selection import GridSearchCV
svm = SVC()
param_grid = {'C':[0.01,0.1,1],'kernel':['rbf','poly','linear','sigmoid'],'gamma':[0.01,0.1,1]}
grid = GridSearchCV(svm,param_grid)
grid.fit(X,y)
print("grid.best_params_ = ",grid.best_params_,", grid.best_score_ =" ,grid.best_score_)

我们可以通过GridSearchCV方法来遍历超参数的各种可能性来寻求最优超参数。这是通过算力碾压的方式暴力调参的手段。当然，在分析问题阶段，我们必须限定了各参数的可选范围才能应用此方法。

因为数据集太简单，我们在遍历第一种可能性时就已经得到100%的准确率了，输出如下：

grid.best_params_ =  {'C': 0.01, 'gamma': 0.01, 'kernel': 'rbf'} , grid.best_score_ = 1.0

总结

当我们处理线性可分的数据集时，可以使用SVC(kernel='linear')方法来训练数据，当然我们也可以使用更快的方法LinearSVC来训练数据，特别是当训练集特别大或特征非常多的时候。

当我们处理非线性SVM分类时，可以使用高斯RBF内核,多项式内核，sigmoid内核来进行非线性模型的的拟合。当然我们也可以通过GridSearchCV寻找最优参数。

往期文章：

• 机器学习(三)：理解逻辑回归及二分类、多分类代码实践
• 机器学习(二)：理解线性回归与梯度下降并做简单预测
• 机器学习(一)：5分钟理解机器学习并上手实践
• 前置机器学习（五）：30分钟掌握常用Matplotlib用法
• 前置机器学习（四）：一文掌握Pandas用法
• 前置机器学习（三）：30分钟掌握常用NumPy用法
• 前置机器学习（二）：30分钟掌握常用Jupyter Notebook用法
• 前置机器学习（一）：数学符号及希腊字母