Optimal Milking（POJ2112+二分+Dinic）

题目链接：http://poj.org/problem?id=2112

题目：

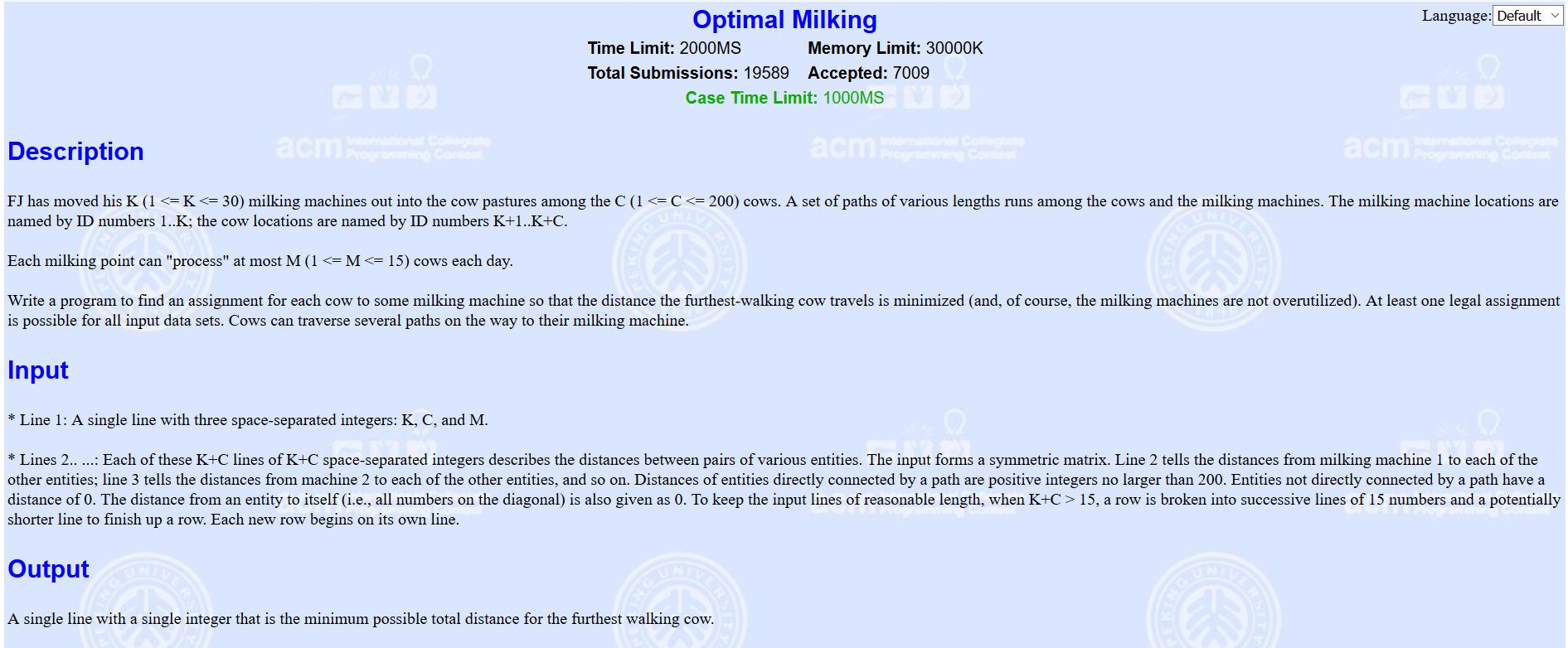
题意：有k台挤奶机，c头奶牛，每台挤奶机每天最多生产m的奶，给你每个物品到其他物品的距离（除了物品到自己本省的距离为0外，两者之间没有路线直接到达也为0，此时需要将距离处理为inf），问跑最远距离的奶牛要跑多远。

思路：先用floyd将各物品间的最短距离求出来，再二分跑最远距离的奶牛走的距离x，将小于x的两者之间进行连边，流量为1，引入一个超级源点和超级汇点，我们采用方向建图的方式，让超级源点与挤奶机连边，且流量为m，奶牛与超级汇点连边，流量为1，跑一边Dinic，如果最大流为c那么ub变成mid-1，否则lb为mid+1。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn =  + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 int k, c, m, s, e, num, tot, maxflow;
 int mp[maxn][maxn], head[maxn], d[maxn];

 queue<int> q;

 struct edge {
     int v, w, next;
 }ed[maxn*maxn];

 void addedge(int u, int v, int w) {
     ed[tot].v = v;
     ed[tot].w = w;
     ed[tot].next = head[u];
     head[u] = tot++;
     ed[tot].v = u;
     ed[tot].w = ;
     ed[tot].next = head[v];
     head[v] = tot++;
 }

 bool bfs() {
     memset(d, , sizeof(d));
     while(!q.empty()) q.pop();
     q.push(s);
     d[s] = ;
     while(!q.empty()) {
         int x = q.front(); q.pop();
         for(int i = head[x]; ~i; i = ed[i].next) {
             int y = ed[i].v;
             if(ed[i].w && !d[y]) {
                 q.push(y);
                 d[y] = d[x] + ;
                 if(y == e) return ;
             }
         }
     }
     return ;
 }

 int dinic(int x, int flow) {
     if(x == e) return flow;
     int rest = flow, k;
     for(int i = head[x]; ~i && rest; i = ed[i].next) {
         int y = ed[i].v;
         if(ed[i].w && d[y] == d[x] + ) {
             k = dinic(y, min(rest, ed[i].w));
             if(!k) d[y] = ;
             ed[i].w -= k;
             ed[i^].w += k;
             rest -= k;
         }
     }
     return flow - rest;
 }

 bool check(int x) {
     tot = ;
     memset(head, -, sizeof(head));
     for(int i = ; i <= k; i++) {
         for(int j = k + ; j <= num; j++) {
             if(mp[i][j] <= x) {
                 addedge(i, j, );
             }
         }
     }
     for(int i = ; i <= k; i++) {
         addedge(s, i, m);
     }
     for(int i = k + ; i <= num; i++) {
         addedge(i, e, );
     }
     int flow = ;
     maxflow = ;
     while(bfs()) {
         while((flow = dinic(s, inf))) maxflow += flow;
     }
     return maxflow == c;
 }

 int main() {
     //FIN;
     scanf("%d%d%d", &k, &c, &m);
     num = k + c;
     for(int i = ; i <= num; i++) {
         for(int j = ; j <= num; j++) {
             scanf("%d", &mp[i][j]);
             if(i != j && mp[i][j] == ) {
                 mp[i][j] = inf;
             }
         }
     }
     for(int k = ; k <= num; k++) {
         for(int i = ; i <= num; i++) {
             for(int j = ; j <= num; j++) {
                 if(mp[i][j] > mp[i][k] + mp[k][j]) {
                     mp[i][j] = mp[i][k] + mp[k][j];
                 }
             }
         }
     }
     s = , e = num + ;
     int ub = inf, lb = , mid;
     while(ub >= lb) {
         mid = (ub + lb) >> ;
         if(check(mid)) ub = mid - ;
         else lb = mid + ;
     }
     printf("%d\n", lb);
     return ;
 }