【推导】【凸包】MIPT-2016 Pre-Finals Workshop, Taiwan NTU Contest, Sunday, March 27, 2016 Problem D. Drawing Hell

平面上n个点，两个人交替决策，用线段连接两个点，但不能跨越其他点或者已经存在的线段。不能做的人算输，问你谁赢。

实际上，跟两个人的决策无关，n个点将平面三角剖分，只需要算出有几条边即可。

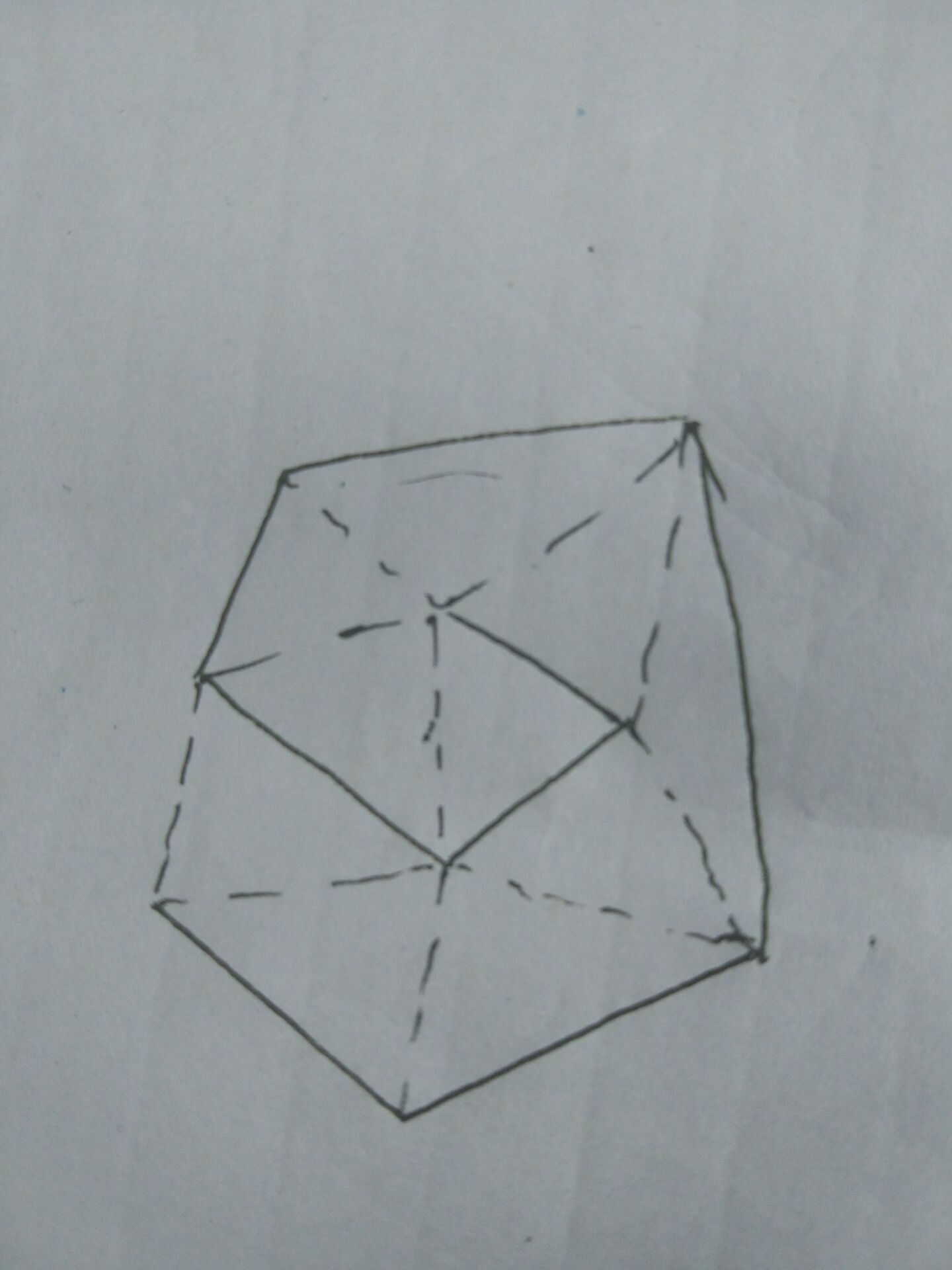
凸包上如果有K个点，那么图中那K-1条实边每条贡献一个三角形。

凸包内其他的边，每条贡献2个三角形。除了最中心那一个贡献一个。

假设总的三角形数是X，那么总的线段数就是(X*3+K)/2。

线段数是奇数就先手胜，否则后手胜。

#include<cstdio>
#include<algorithm>
using namespace std;
struct Point{
	int x,y;
	Point(const int &x,const int &y){
		this->x=x;
		this->y=y;
	}
	Point(){}
	void read(){
		scanf("%d%d",&x,&y);
	}
}p[1005],q[1005];
typedef Point Vector;
Vector operator - (const Point &a,const Point &b){
	return Vector(a.x-b.x,a.y-b.y);
}
int Cross(const Vector &a,const Vector &b){
	return a.x*b.y-a.y*b.x;
}
bool cmp(const Point &a,const Point &b){
	return a.x!=b.x ? a.x<b.x : a.y<b.y;
}
int n,K,T;
int main(){
//	freopen("d.in","r",stdin);
	scanf("%d",&T);
	for(;T;--T){
		K=0;
		scanf("%d",&n);
		for(int i=0;i<n;++i){
			p[i].read();
		}
		sort(p,p+n,cmp);
		bool flag=1;
		for(int i=1;i<n-1;++i){
			if(Cross(p[i+1]-p[i],p[i]-p[i-1])!=0){
				flag=0;
				break;
			}
		}
		if(flag){
			puts((n-1)%2==1 ? "T^T" : "OwO");
			continue;
		}
		for(int i=0;i<n;++i){
			while(K>1 && Cross(q[K-1]-q[K-2],p[i]-q[K-1])<0){
				--K;
			}
			q[K++]=p[i];
		}
		for(int i=n-2,t=K;i>=0;--i){
			while(K>t && Cross(q[K-1]-q[K-2],p[i]-q[K-1])<0){
				--K;
			}
			q[K++]=p[i];
		}
		--K;
		int A=K-1;
		int B=n-K-1;
		int sjxs=A+B*2+1;
		puts((sjxs*3+K)/2%2==1 ? "T^T" : "OwO");
	}
	return 0;
}