【7】Manacher算法学习笔记

前言

Manacher 算法是最好写的字符串算法。——教练

暴力求法

---

给出一个只由小写英文字符 \(\texttt a,\texttt b,\texttt c,\ldots\texttt y,\texttt z\) 组成的字符串 \(S\)，求 \(S\) 中最长回文串的长度 。

---

暴力算法 \(1\)：

枚举左右端点，\(O(n)\) 判断是否为回文串，时间复杂度 \(O(n^3)\)。

暴力算法 \(2\)：

枚举中间点（包括字符与字符之间的空隙），根据回文串的性质，向左右两边扩展。如果左右并不相等，立即结束并更新答案；否则将左右各推一个字符，当前答案自增。时间复杂度 \(O(n^2)\)。

但是，此题的数据范围是 \(1\le |S|\le 1.1\times 10^7\)。

Manacher 算法

预处理

Manacher 算法是基于暴力算法 \(2\) 的再优化，由于回文串的对称中心有可能会在两个字符之间的空隙处，所以我们可以插入一些特殊字符，例如 #。为了避免越界，我在字符串开头也插入了一个特殊字符 !。

下标从 \(1\) 开始。

由于格式影响，代码中与 \(\LaTeX\) 公式相冲突的字符改为了 !。

scanf("%s",stri);
int l=strlen(stri);
str[0]='!';
for(int i=0;i<l;i++)
	{
	   str[i*2+1]='#';
	   str[i*2+2]=stri[i];
	}
str[l*2+1]='#';
l=l*2+1;

最长回文延伸长度

以 \(i\) 为中心的最长回文延伸长度，记作 \(p[i]\)。

例如，字符串 abaaabaa 的 p 数组：

	a	b	a	a	a	a	b	a	a
\(p[i]\)	\(1\)	\(2\)	\(1\)	\(2\)	\(2\)	\(1\)	\(3\)	\(1\)	\(1\)

注意一个字符也算回文串，所以 \(p[i]\) 的最小值为 \(1\)。

可以知道，对于每个位置 \(i\)，以 \(i\) 为中心的最长回文串的起始位置为 \(i-p[i]+1\)，结束位置为 \(i+p[i]-1\)。

算法流程

由于回文串在回文中心左右的部分完全对称，我们可以考虑从这一点来优化算法，进行递推。Manacher 算法的递推方向就是从左到右。（下标从 \(1\) 开始）

\(1\)：最理想的情况

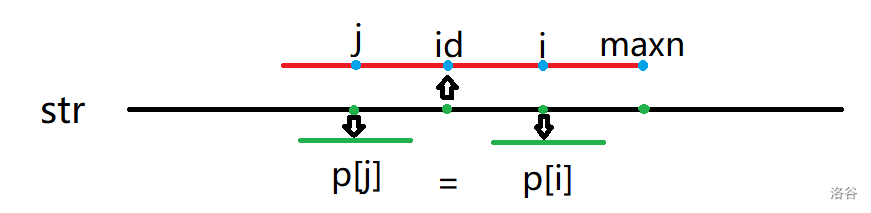
（自绘插图，略显粗糙）

如图，\(maxn\) 表示目前求出的回文串中最远延伸的点，而 \(id\) 表示这个字符串的对称中心。点 \(i\) 是我们正在求的点，点 \(j\) 是关于 \(mid\) 的对称点。由回文串的对称性可以得出 \([id-p[id]+1,id]\) 和 \([id,id+p[id]-1]\) 两段一定完全相等，进一步推出以 \(j\) 为回文中心的串一定与以 \(i\) 为回文中心的串完全相等，所以 \(p[i]=p[j]\)。

因为 \(j\) 一定在 \(i\) 之前，符合递推的条件。\(j\) 的坐标可以 \(O(1)\) 求出，由坐标中点公式得出 \(j=id\times 2-i\)，整个这种情况下的转移就可以 \(O(1)\) 实现了。

\(2\)：不是很理想的情况

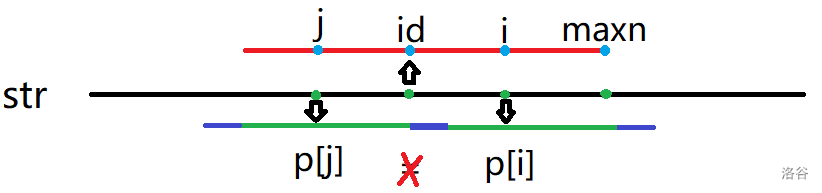
\(p[j]\) 出界的部分不能保证与 \(p[i]\) 出界的部分完全相同，此时 \(p[i]\) 不一定等于 \(p[j]\)。但是我们可以知道在 \([id-p[id]+1,id+p[id]-1]\) 这个范围内的部分完全相等，也就是说，在不超过这个范围的部分，以 \(j\) 为回文中心的串一定与以 \(i\) 为回文中心的串完全相等，观察以下图，其实就是 \(maxn-i+1\)。剩下的，就朴素吧。

由于每次朴素之后会把 \(maxn\) 往后推，所以时间复杂度还是 \(O(n)\)。

\(3\)：很不理想的情况

无能为力了，只能朴素了。由于每次朴素之后会把 \(maxn\) 往后推，所以时间复杂度还是 \(O(n)\)。

具体实现的时候，可以首先判定是否为情况 \(3\)，然后可以直接用一个 \(min\) 函数处理出情况 \(1\) 和情况 \(2\)。因为当处于情况 \(2\) 时，情况 \(2\) 的数值小于情况 \(1\)；而处于情况 \(1\) 时,情况 \(1\) 的数值小于情况 \(2\)。最后在结合插入字符，朴素比较即可，注意更新 \(maxn\) 和 \(id\)。

这里实现时，\(maxn\) 的值是 \(i+p[i]\)，是可以取到的最后一个位置的后一个位置，是不能取到的。所以代码中才写 \(maxn>i\)，\(maxn-i\)，这样写是为了节约一点点码量，但实际中不建议这么写，容易被误解。

p[1]=1;maxn=0;id=0;
for(int i=1;i<=l;i++)
	{
	if(maxn>i)p[i]=min(p[id*2-i],maxn-i);
	else p[i]=1;
   while(str[i-p[i]]==str[i+p[i]])p[i]++;
	if(i+p[i]>maxn)maxn=i+p[i],id=i;
	}

由于插入字符的影响，我们注意到 \(p[i]-1\) 就是以 \(i\) 为中心的最长回文子串的长度，直接遍历一遍求最大值，就在 \(O(n)\) 的时间内解决了问题。

例题

例题 \(1\) ：

P3805 【模板】manacher 算法

Manacher 模板题，不多赘述。

#include <bits/stdc++.h>
using namespace std;
int p[22000010],maxn=0,id=0,ans=0;
char stri[11000010],str[22000010];
int main()
{
	scanf("%s",stri);
	int l=strlen(stri);
	str[0]='!';
	for(int i=0;i<l;i++)
	    {
	    	str[i*2+1]='#';
	    	str[i*2+2]=stri[i];
		}
	str[l*2+1]='#';
	l=l*2+1;
	p[1]=1;maxn=0;id=0;
	for(int i=1;i<=l;i++)
	    {
	    	if(maxn>i)p[i]=min(p[id*2-i],maxn-i);
	    	else p[i]=1;
	    	while(str[i-p[i]]==str[i+p[i]])p[i]++;
	    	if(i+p[i]>maxn)maxn=i+p[i],id=i;
		}
	for(int i=1;i<=l;i++)
	    ans=max(p[i]-1,ans);
	printf("%d",ans);
	return 0;
}

例题 \(2\) ：

P1659 [国家集训队]拉拉队排练

看到题目中提到了回文串，自然联想到 Manacher 算法。

首先，如果一个回文串的长度为 \(n\)（\(n\) 为奇数且 \(n\ge1\)），则这个串同样也可以算作一个长度为 \(n-2\) 的回文串。因为这个回文串可以删去其最左右两边的两个字符，变成长度为 \(n-2\) 的串。由于原串是回文串，所以删去的字符相同，新串依旧是回文串。

有了这点，我们很容易得到一个思路：首先求出每个位置的最长回文子串，用一个桶记录下来。然后降序枚举（保证从高到低）最长回文子串长度，并进行数量累加，结果累乘，然后用快速幂求出值即可。

#include <bits/stdc++.h>
using namespace std;
long long p[2000020],t[2000020],maxn=0,id=0,ans=1,l=0,k=0,tj=0,tu=0,now=0,mod=19930726;
char stri[1000010],str[2000020];
long long power(long long a,long long p,long long m)
{
	long long x=a,ans=1;
	while(p)
	    {
	    	if(p%2==1)ans=ans*x%m;
	    	p/=2;
	    	x=x*x%m;
		}
	return ans;
}

int main()
{
	scanf("%lld%lld",&l,&k);
	scanf("%s",stri);
	str[0]='!';
	for(int i=0;i<l;i++)
	    {
	    	str[i*2+1]='#';
	    	str[i*2+2]=stri[i];
		}
	str[l*2+1]='#';
	l=l*2+1;
	p[1]=1;maxn=0;id=0;
	for(int i=1;i<=l;i++)
	    {
	    	if(maxn>=i)p[i]=min(p[id*2-i],maxn-i);
	    	else p[i]=1;
	    	while(str[i-p[i]]==str[i+p[i]])p[i]++;
	    	if(i+p[i]>maxn)maxn=i+p[i],id=i;
		}
	for(int i=1;i<=l;i++)p[i]--;
	for(int i=1;i<=l;i++)t[p[i]]++;
	for(int i=1000020;i>0;i--)
	    {
	    	if(i%2==1)
	    	   {
			   tj+=t[i];
			   if(tj==0)continue;
			   if(now+tj<=k)ans=ans*power(i,tj,mod)%mod,now+=tj;
			   else
			      {
			      	ans=ans*power(i,k-now,mod)%mod;
			      	printf("%lld",ans);
			      	return 0;
				  }
		       }
		}
	return 0;
}

例题 \(3\) ：

P5446 [THUPC2018]绿绿和串串

由翻转操作的定义，得知翻转后的字符串一定是长度为奇数的回文串，再次联想到 Manacher。由于回文串长度为奇数，所以不用在空隙处插入字符。

性质 \(1\)：如果一个位置 \(i\)，其最长回文串延伸到字符串末尾，那么这个位置一定可以取到。

证明：

设字符串为 \(S\)，如果这个位置可以取到，最终翻转形成的串一定为 \(Q+S_i+Q\)（\(Q\) 为 \(i\) 前所有字符组成的字符串）。因为其最长回文串延伸到字符串末尾，设不算位置 \(i\) 的单边的回文部分为 \(H\)，则原字符串可以写作：（\(Q_0=Q-H\)）

\[Q_0+H+S_i+H
\]

最终翻转形成的串可以写作：

\[Q_0+H+S_i+H+Q_0
\]

因为给出的字符串可以是最终翻转形成的字符串的前缀，对比二式发现给出的字符串一定为最终翻转形成的字符串的前缀，所以这个位置可以取到，结论得证。

性质 \(2\)：在不属于性质 \(1\) 的前提下，如果一个位置 \(i\)，其最长回文串向左延伸到字符串第一个字符，向右延伸到可以取到的位置，那么这个位置一定可以取到。

证明：

由于不属于性质 \(1\)，所以必须回文串从头开始，否则无法保证回文部分之前的字符与之后的字符完全相等，所以要求最长回文串向左延伸到字符串第一个字符。

如果最长回文串向右延伸到可以取到的位置，那么相当于再翻转后的字符串是符合要求的，所以这个能翻转出符合要求的字符串的位置也是符合要求的。又因为最长回文串向左延伸到字符串第一个字符，所以不会对再翻出的符合要求的字符串造成影响，结论得证。

因此，我们可以结合上面两条性质，从右往左进行递推。对于每一个点，首先判断其是否符合性质 \(1\)，然后判断其是否符合性质 \(2\)。同时为了方便计算性质 \(2\)，可以用一个数组记录每个位置是否可行。最后遍历一遍，输出可行的位置即可。

upd on 2024/8/9：更新了代码，原本的代码会被 hack。

#include <bits/stdc++.h>
using namespace std;
long long t,p[6000000],maxn=0,id=0,ans=0,book[6000000];
char s[6000000];
int main()
{
	scanf("%d",&t);
	while(t--)
	   {
		scanf("%s",s+1);
		s[0]='$';
		long long l=strlen(s);
		for(int i=1;i<=l;i++)p[i]=book[i]=0;
		s[l+1]='#',l--,p[1]=1,maxn=0,id=0;
		for(int i=1;i<=l;i++)
		    {
		    	if(maxn>i)p[i]=min(p[id*2-i],maxn-i);
		    	else p[i]=1;
		    	while(s[i-p[i]]==s[i+p[i]])p[i]++;
		    	if(i+p[i]>maxn)maxn=i+p[i],id=i;
			}
		for(int i=l;i>0;i--)
		    if(i+p[i]==l+1)book[i]=1;
		    else if(i==p[i])book[i]=book[i+p[i]-1];
		for(int i=1;i<=l;i++)
		    if(book[i])printf("%d ",i);
		printf("\n");
        }
	return 0;
}

后记

算法只是工具，现在很少直接考单纯的算法。Manacher 的题目重要的不是 Manacher 算法本身，而是其后的思维难度。——教练