Educational Codeforces Round 104 (Rated for Div. 2) A~E题解

写在前边

链接：Educational Codeforces Round 104 (Rated for Div. 2)

A. Arena

链接：A题链接

题目大意:

给定一个长度为\(n\)的数组，表示\(n\)个英雄的初始积分，任意选两英雄作战，积分高的获胜，同时积分高的那个积分还会增加\(1\)，问有多少个英雄可以获胜。

思路：

明显，最低分的那个英雄永无出头之日，所以只需要排个序，让其他英雄与最低分的英雄作战即可。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

const int N = 110;
int a[N];

void solve() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];

    sort(a, a + n);

    int res = 0;
    for (int i = n - 1; i >= 1; i--) {
        if (a[i] > a[0]) res++;
    }

    cout << res << endl;
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }

    return 0;
}

B. Cat Cycle

链接：B题链接

题目大意:

一只大猫一只小猫不停的换位置睡觉，大猫的睡觉位置变化为\(n,n-1,n-2,...,1\)，小猫的睡觉位置变化为\(1, 2, 3, ...,n-1, n-2\)，小猫不能和大猫睡到一起，一旦遇见小猫必须跳过当前位置到下一个位置，即如果在\(1\)遇到大猫，那么应该立即跳到\(2\)，求在两者各自移动\(k\)个位置后小猫在哪个位置。

思路：

可以看成两只猫背靠背朝反方向移动，如果是偶数，那么两者永远不会相遇，如果是奇数，那么很神奇的是每\(\lfloor \cfrac{n}{2} \rfloor\)步两者就会相遇，那么小猫需要跳一步，更神奇的是这时两者又背靠背挨着了，向反方向移动，即小猫恰好在大猫后一个数，换句话说，就是说小猫每\(\lfloor \cfrac{n}{2} \rfloor\)就会多跳一步那么令\(t = \cfrac{n}{2}\)为一个周期，那么小猫就多跳了\(\lfloor \cfrac{k}{t} \rfloor\)步，所以它处于的位置就是\((k + \lfloor \cfrac{k}{t} \rfloor) \,\, mod \,\, n\)

那么把两种情况融合就是:

\[(k + (n \,\, mod \,\, 2)\lfloor \cfrac{k}{t} \rfloor) \,\, mod \,\, n （从0开始索引）
\]

还有一个细节就是，上面公式只适合从\(0\)开始索引，如果像本题这样从\(1\)开始索引，那么可以先让\(k\)减\(1\)，然后\(mod \, n\)后再加\(1\)，看下面代码。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

void solve() {
    int n, k;
    scanf("%d%d", &n, &k);
    k--;
    if (n % 2 == 0) {
        printf("%d\n", k % n + 1);
        return;
    }
    int t = n / 2; //一个周期
    printf("%d\n", (k + k / t) % n + 1);
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }

    return 0;
}

C. Minimum Ties

链接：C题链接

题目大意:

有n支队伍，要进行\(\cfrac{n*(n-1)}{2}\)场比赛，即比如有3支队伍，有\(1\)-\(2\),\(1\)-\(3\),\(2\)-\(3\)三场比赛，胜者得\(3\)分，平局各得\(1\)分，败者不得分，现在要求我们通过让他们之间进行最少的平局使得所有队伍获得相同的分数。

思路：

首先明白，如果没有平局得情况下，那么所有队伍得分和为\(sum = \cfrac{3*n*(n-1)}{2}\)，那么对于有奇数支队伍的时候，\(sum\)可以被\(n\)整除，所以对于奇数支来说，就让他们输赢对半分即可，把它们看成一个图上的几个点，当前队伍赢得它前边\(\lfloor \cfrac{n}{2} \rfloor\)支队伍，输给其他队伍，那么这样就构成了一个欧拉图(明天补)，假如有五支队伍，一个点的出边所连的点表示他干掉的队伍，指向它的点表示干掉它的队伍，那么构造答案即可。

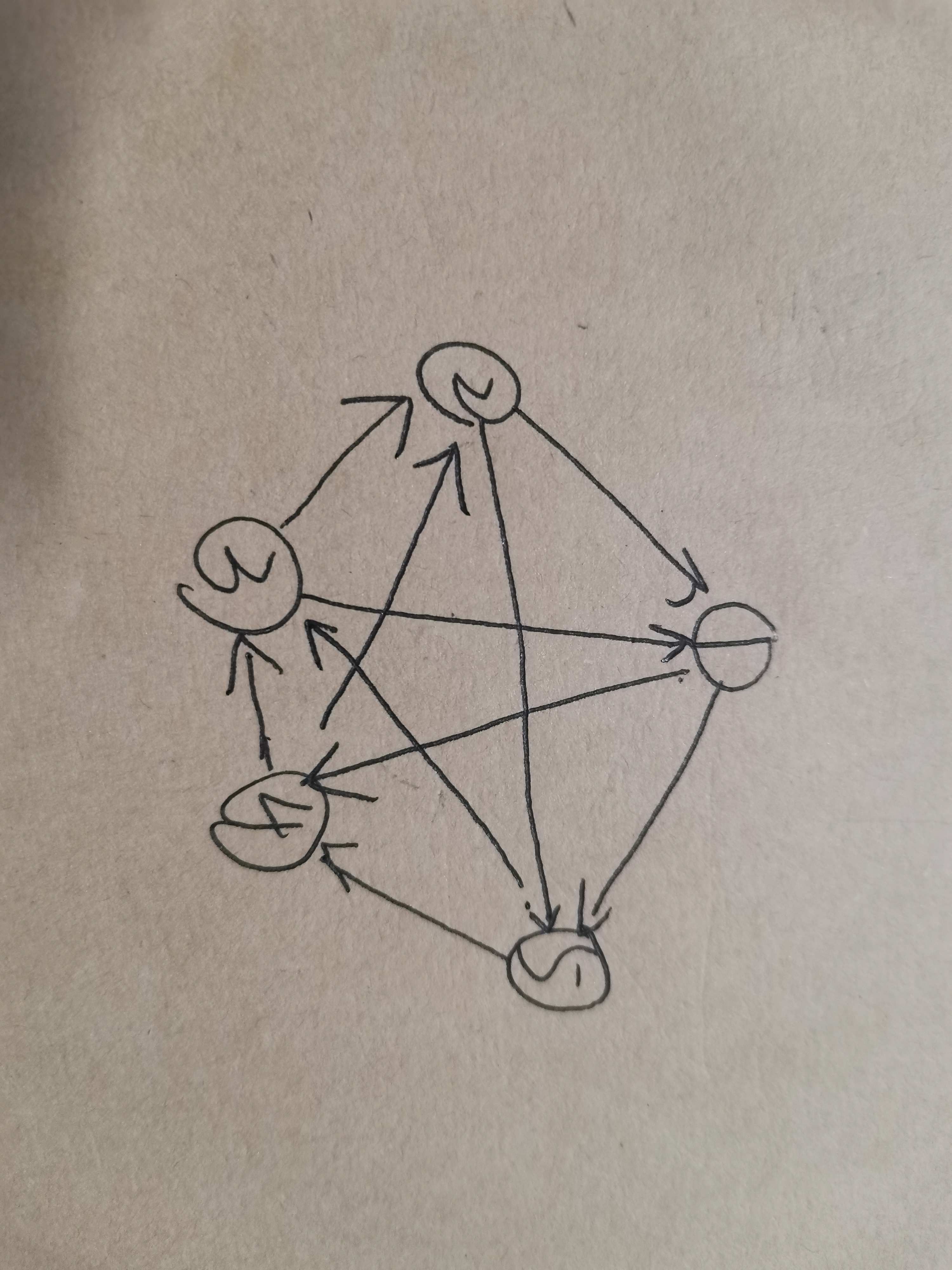
对于\(n\)为偶数情况下，是不能这样搞的，因为会发现\(sum\)无法被\(n\)整除，所以我们可以通过让它们之间产生平局来使\(sum\)被\(n\)整除，假设产生\(t\)个平局，一个平局则让总分减少1，那么要使得\(\cfrac{3n(n-1)}{2} - t\)被\(n\)整除，可得\(t = n / 2\)，因为\((\cfrac{3n(n-1)}{2} + 2n) \,\, mod \,\, n = \cfrac{n}{2}\),注意这里加\(2n\)再取模是为了让余数得到正数（刚学到的技巧），同时只有\(n\)为偶数时这种情况下的公式才可以成立，不然得到\(-\cfrac{n}{2}\)就意味着我们需要给总分加分，显然不合理。这样之后我们就知道，需要进行\(\cfrac{n}{2}\)场平局，那么还是可以看成一个图，让每个队伍战胜它前边第\(\cfrac{n}{2}\)支队伍前的队伍，输掉它后边第\(\cfrac{n}{2}\)支队伍后的队伍，对于恰好它前边恰好第\(\cfrac{n}{2}\)支队伍打成平局，那么这样平局恰好是\(\cfrac{n}{2}\)场。

构造答案即可。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

void solve() {
    int n;
    cin >> n;
    if (n % 2 == 1) {
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (j - i <= n / 2) {
                    cout << 1 << " ";
                } else {
                    cout << -1 << " ";
                }
            }
        }
        puts("");
    } else {
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (j - i < n / 2) {
                    cout << 1 << " ";
                } else if (j - i == n / 2) {
                    cout << 0 << " ";
                } else {
                    cout << -1 << " ";
                }
            }
        }
        puts("");
    }
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }
    return 0;
}

D. Pythagorean Triples

链接：D题链接

题目大意:

找出一个三元组\(1 \leq a \leq b \leq c \leq n\)，使得满足\(c^2 = a^2 + b^2\)与\(c = a^2 - b\)。

思路：

推公式，两方程联立得:\(c(c- 1) = b(b+1)\)，那么可得\(c = b + 1\)，那么带入\(c = a^2 - b\)得到\(a^2 = 2b + 1\)。那么可以看出，有唯一\(b\)对应唯一的奇数\(a^2(\geq 3)\)，那么我们就枚举所有的\(a\)即可，同时要求\(c < n\)，即要求\(b < n - 1\)，那么，\(a^2\)最多就到\(2*n - 1\)即可。复杂度约为\(O(\sqrt{n})\)

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

void solve() {
    int res = 0, n;
    scanf("%d", &n);
    for (int i = 3; i * i <= 2 * n - 1; i += 2) res++;

    printf("%d\n", res);
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }

    return 0;
}

E. Cheap Dinner

链接：E题链接

题目大意:

有四类菜，每类菜又有多种，给定它们的价格，同时在第一类与第二类，第二类与第三类，第三类与第四类之间还存在冲突，我们从四类菜种各选一类菜，要求它们之间不能有冲突，并且我们花费的价格最小。

思路：

参考博客：颜椒^, 随处可见的阿宅

本质就是数字三角形\(DP\)吧，不过不一样的是这题加了一下限制。

用\(dp[i][j]\)表示走到第\(i\)类菜的第\(j\)道菜获得的最小代价,所以得到方程就是:

\[dp[i][j] = dp[i - 1][k] + prices[i][j]
\]

而我们要快速得到最优的\(dp[i - 1][k]\)，肯定不能用枚举的方式，可以用\(map\)来存所用到的每一类菜价格，同时记录关联，有关联的菜品会先从\(map\)中删除，由于\(map\)会自动排序，那么\(map\)中剩余的第一个元素就是我们所需要的。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3,"Ofast","inline")

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

const int Mod = 10000007;

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}
const int N = 150010;
const int INF = 1e9;
int n[5];
int dish[5][N];
vector<int> relation[5][N];

void solve() {
    for (int i = 1; i <= 4; i++) scanf("%d", &n[i]);
    for (int i = 1; i <= 4; i++) {
        for (int j = 1; j <= n[i]; j++) {
            scanf("%d", &dish[i][j]);
        }
    }

    int m;
    for (int i = 2; i <= 4; i++) {
        scanf("%d", &m);
        for (int j = 1; j <= m; j++) {
            int v1, v2;
            scanf("%d%d", &v1, &v2);
            relation[i][v2].push_back(v1); //后一类的第v2道菜与前一类的第v1道有关联
        }
    }

    for (int i = 2; i <= 4; i++) { //从第二类菜开始处理
        map<int, int> st; //map有自动排序功能
        for (int j = 1; j <= n[i - 1]; j++) st[dish[i - 1][j]]++; //预处理前一类菜的价格

        for (int j = 1; j <= n[i]; j++) {
            for (auto &k : relation[i][j]) {
                st[dish[i - 1][k]]--; //删去有关联的
                if (!st[dish[i - 1][k]]) st.erase(dish[i - 1][k]);
            }
            if (st.size()) dish[i][j] += st.begin()->first;
            else dish[i][j] = INF;
            for (auto &k : relation[i][j]) st[dish[i - 1][k]]++; //恢复
        }
    }
    int res = INF;
    for (int i = 1; i <= n[4]; i++) {
        res = min(res, dish[4][i]);
    }
    if (res == INF) puts("-1");
    else printf("%d\n", res);
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    solve();

    return 0;
}