2021-08-26：长度为N的数组arr，一定可以组成N^2个数字对。例如arr = [3,1,2]，数字对有(3,3) (3,1) (3,2) (1,3) (1,1) (1,2) (2,3) (2

2021-08-26：长度为N的数组arr，一定可以组成N^2个数字对。例如arr = [3,1,2]，数字对有(3,3) (3,1) (3,2) (1,3) (1,1) (1,2) (2,3) (2,1) (2,2)，也就是任意两个数都可以，而且自己和自己也算数字对，数字对怎么排序？第一维数据从小到大；第一维数据一样的，第二维数组也从小到大，所以上面的数值对排序的结果为：(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)。给定一个数组arr，和整数k，返回第k小的数值对。

福大大 答案2021-08-26：

1.暴力解。
时间复杂度：(N^2 * log(N^2)).
2.下标定位+bfprt算法。
2.1.k–。
2.2.定位下标i1和i2。
i1=k/N。
i2=k%N。
2.3.根据bfprt算法求出第i1小和第i2小的数。
时间复杂度：O(N)。
空间复杂度：O(1)。arr数组里的元素顺序会发生变化。

代码用golang编写。代码如下：

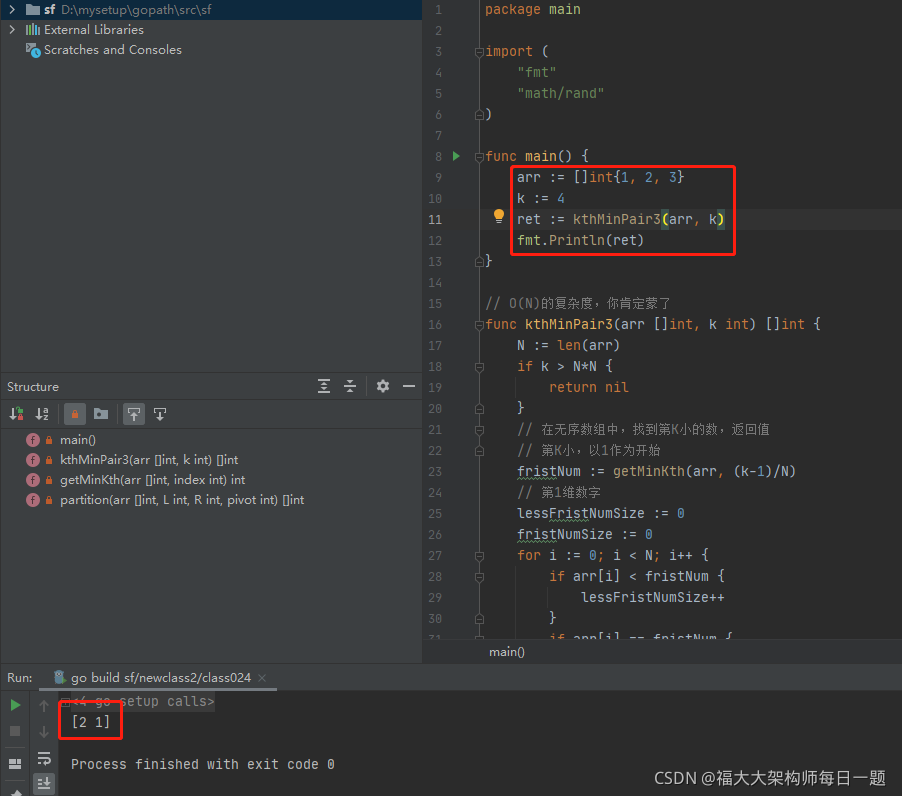
package main

import (
    "fmt"
    "math/rand"
)

func main() {
    arr := []int{1, 2, 3}
    k := 4
    ret := kthMinPair3(arr, k)
    fmt.Println(ret)
}

// O(N)的复杂度，你肯定蒙了
func kthMinPair3(arr []int, k int) []int {
    N := len(arr)
    if k > N*N {
        return nil
    }
    // 在无序数组中，找到第K小的数，返回值
    // 第K小，以1作为开始
    fristNum := getMinKth(arr, (k-1)/N)
    // 第1维数字
    lessFristNumSize := 0
    fristNumSize := 0
    for i := 0; i < N; i++ {
        if arr[i] < fristNum {
            lessFristNumSize++
        }
        if arr[i] == fristNum {
            fristNumSize++
        }
    }
    rest := k - (lessFristNumSize * N)
    return []int{fristNum, getMinKth(arr, (rest-1)/fristNumSize)}
}

// 改写快排，时间复杂度O(N)
// 在无序数组arr中，找到，如果排序的话，arr[index]的数是什么？
func getMinKth(arr []int, index int) int {
    L := 0
    R := len(arr) - 1
    pivot := 0
    var range2 []int
    for L < R {
        pivot = arr[L+rand.Intn(R-L+1)]
        range2 = partition(arr, L, R, pivot)
        if index < range2[0] {
            R = range2[0] - 1
        } else if index > range2[1] {
            L = range2[1] + 1
        } else {
            return pivot
        }
    }
    return arr[L]
}

func partition(arr []int, L int, R int, pivot int) []int {
    less := L - 1
    more := R + 1
    cur := L
    for cur < more {
        if arr[cur] < pivot {
            less++
            arr[less], arr[cur] = arr[cur], arr[less]
            cur++
        } else if arr[cur] > pivot {
            arr[cur], arr[more] = arr[more], arr[cur]
            more--
        } else {
            cur++
        }
    }
    return []int{less + 1, more - 1}
}

执行结果如下：

---

左神java代码