剑指offer51(Java)-数组中的逆序对（困难）

题目：

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例1：

输入: [7,5,6,4]

输出: 5

限制：

0 <= 数组长度 <= 50000

解题思路：

这道题的核心在于 归并排序，在归并排序的基础上进行求解 逆序对。

题解参考 K神老师的题解和 liweiwei1419老师的讲解视频，这道题对于我来说有点困难~

归并排序的核心在于分治思想：

• 分： 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
• 治： 划分到子数组长度为 1 时，开始向上合并，不断将 较短排序数组 合并为 较长排序数组，直至合并至原数组时完成排序。

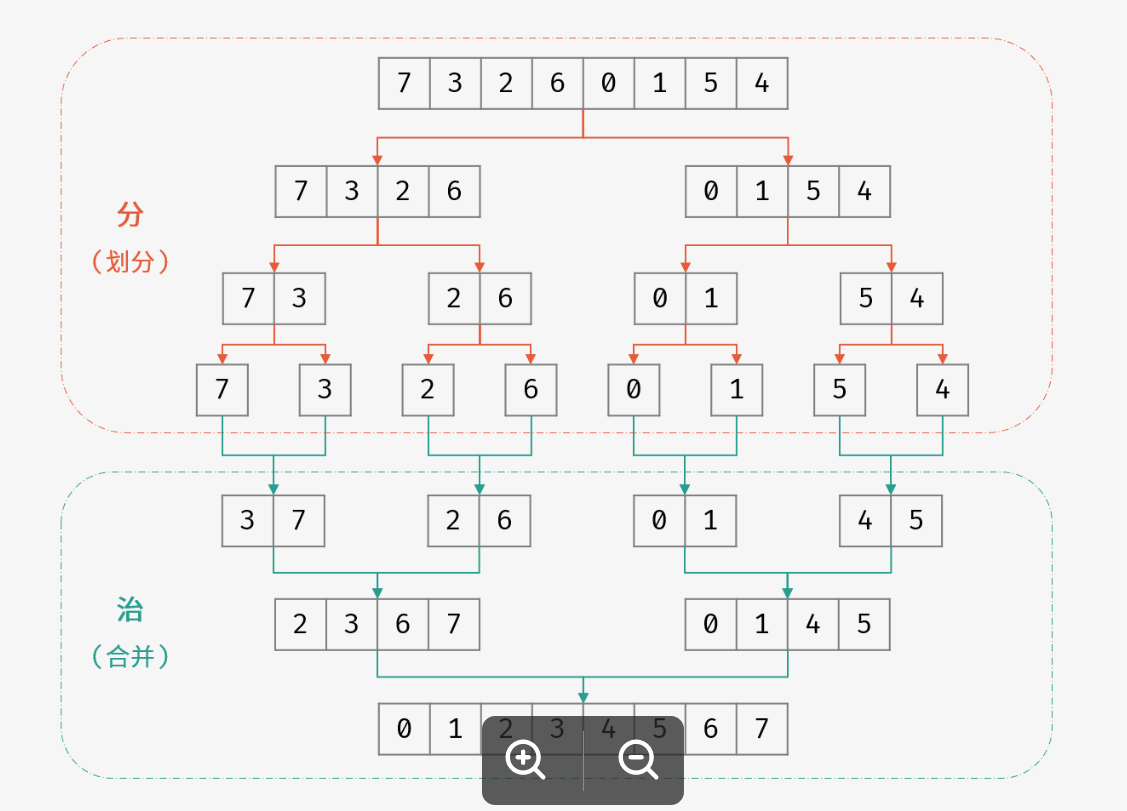
大致思想：

主函数reversePairs():

1.执行差分数组方法mergeSort()

2.返回逆序对总数

差分数组mergeSort()：

1.将数组一份为二，进行递归拆分；

2.执行归并排序merge()，并统计逆序对的个数。

 归并排序merge()：

1.定义一个临时数组，用于统计合并过程中的临时数组；

2.设置双指针 i 和 j 分别指向左右子数组的首元素即 i = left , j = mid+1，设置t=0指向临时数组下标:

• nums[i] <= nums[j]：说明左子数组的元素小于右子数组，此时不存在逆序对，直接将nums[i]放入temps[t]，执行 i++,j++；（类似于下图情况）

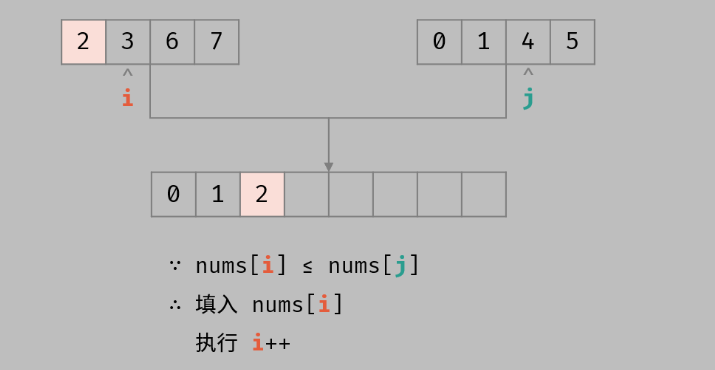
• 否则 nums[i] > nums[j]：说明左子数组及左子数组剩下的元素都大于右子数组元素，则将小的nums[j]放入temps[t]，并执行j++,t++,逆序数对数加 m-i+1个（类似于下图情况）

• 当 i <= mid 时(j > right)，代表右子数组已经合并完，剩余的左子数组加入到temp后面即可；
• 当 j <= right 时(i>mid),代表左子数组已经合并完，剩余的右子数组加入到temp后面即可。

• 最后需要将每一轮排好序的数组放回原数组。

疑惑：nums[left + k] = temp[k]：因为合并方法merge()中的left根据每一次递归都不一样的，故每一次排好序的数都应该从left开始放。

代码：

 1 class Solution {
 2     //定义一个全局变量用于计算逆序对的个数
 3     int count = 0;
 4     public int reversePairs(int[] nums) {
 5         mergeSort(nums, 0, nums.length-1);
 6         return count;
 7     }
 8     //将数组拆分
 9     public void mergeSort(int[] nums,int left,int right){
10         //如果只有一个或空则直接退出
11         if (left >= right) return;
12         int mid = (left + right) /2;
13         //对左边进行拆分
14         mergeSort(nums, left, mid);
15         //对右边进行拆分
16         mergeSort(nums, mid+1, right);
17         //合并
18         merge(nums,left,right,mid);
19     }
20     //合并方法
21     public void merge(int[] nums,int left,int right,int mid){
22         //定义一个临时数组
23         int[] temp = new int[right-left+1];
24         //定义指针指向第一个数组的第一个元素
25         int i = left;
26         //定义指针指向第二个数组的第一个元素
27         int j = mid+1;
28         //定义一个指针指向临时数组的第一个元素
29         int t = 0;
30         //当两数组都有数据的时候进行遍历
31         while (i <= mid && j <= right){
32             //如果第一个数组元素小，那么就直接将小的放入临时数组
33             if(nums[i] <= nums[j]){
34                 temp[t++] = nums[i++];
35             }else{
36                 //如果第一个数组元素大，那么就要将小的先放，并统计逆序对的个数
37                 count += mid-i+1;
38                 temp[t++] = nums[j++];
39             }
40         }
41         //当右边的数组已经遍历完，左边还剩余的时候，直接将剩余元素加入临时数组
42         while (i <= mid){
43             temp[t++] = nums[i++];
44         }
45         //当左边的数组已经遍历完，右边还剩余的时候，直接将剩余元素加入临时数组
46         while (j <= right){
47             temp[t++] = nums[j++];
48         }
49         //用临时数组的值去覆盖原数组的值
50         for(int k = 0; k < temp.length; k++){
51             nums[left + k] = temp[k];
52         }
53     }
54 }