P4174 [NOI2006]最大获利 (最大权闭合子图)

P4174 [NOI2006]最大获利 (最大权闭合子图)

题目链接

题意

建\(i\)站台需要\(p_i\)的花费，当\(A_i,B_i\)都建立时获得\(C_i\)的利润，求最大的利润

思路

最大权闭合子图模板题

参考论文

将所有站台与S连接，边权值为\(P_i\),将第\(i\)个利润与\(T\)连接，边权为\(C_i\),再与\(A_i,B_i\)连接，边权为\(inf\),跑网络流,最小割 = 建立站台的花费 + 不要的利润 ，Ans = 所有的利润 - (建立站台的花费 + 不要的利润) = 所有的利润 - 最小割

最小割 = 最大流

样例图

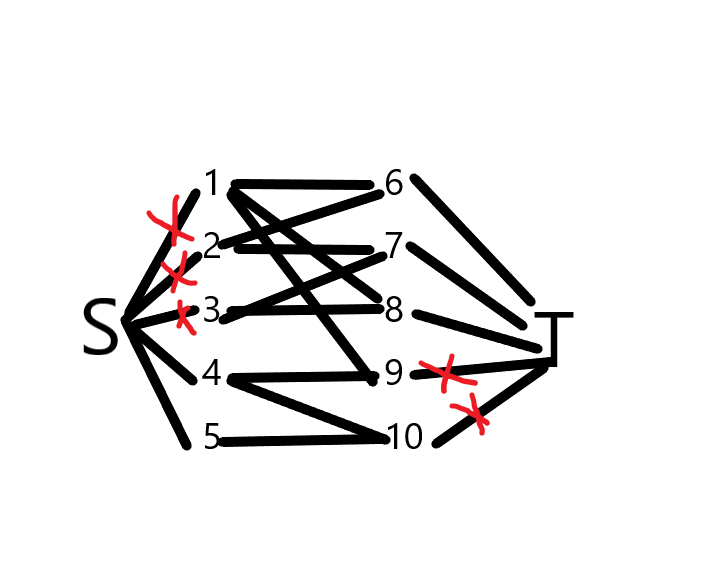
代码

#include <bits/stdc++.h>
using namespace std;
const int inf = 1<<30;
const int N = 55500;
const int M = 502020;
int f[N], w[M], nxt[M], to[M], h[N];
int num;
void add(int x,int y,int z)
{
	to[++num] = y;
	w[num] = z;
	nxt[num] = f[x];
	f[x] = num;
	to[++num] = x;
	w[num] = 0;
	nxt[num] = f[y];
	f[y] = num;
}
int bfs(int s,int t)
{
	memset(h,0,sizeof(h));
	h[s] = 1;
	queue <int > q;
	q.push(s);
	while (!q.empty())
	{
		int x = q.front();
		q.pop();
		for (int i = f[x]; i; i = nxt[i])
		{
			int y = to[i];
			if (!h[y] && w[i])
			{
				h[y] = h[x] + 1;
				q.push(y);

			}
		}
	}
	if (!h[t] ) return 0;
	else return 1;
}
int dfs(int x,int t,int flow)
{
    if(x==t) return flow;
    int fl=0;
    for(int i=f[x]; i && flow ;i=nxt[i])
    {
        if(h[to[i]]==h[x]+1&&w[i])
        {
            int mi=dfs(to[i],t,min(w[i],flow));
            w[i]-=mi; w[i^1]+=mi; fl+=mi; flow-=mi;
        }
    }
    if(!fl)    h[x]=-1;
    return fl;
}
long long dinic(int s,int t)
{
	long long ret = 0;
	while (bfs(s,t)) ret += dfs(s,t,inf);
	return ret;
}
int main()
{
	ios::sync_with_stdio(false);
	int n,m;
	cin >> n >> m;
	num = 1;
	for (int i = 1; i <= n; i++)
	{
		int x;
		cin >> x;
		add(0,i,x);
	}
	long long tot = 0;
	for (int i = 1; i <= m; i++)
	{
		int x, y, z;
		cin >> x >> y >> z;
		tot += z;
		add(x,i+n,inf);
		add(y,i+n,inf);
		add(i+n,m+n+1,z);
	}
	cout << tot - dinic(0,n+m+1) << endl;
}