agc004E Salvage Robots

题意：

一个网格图，有若干机器人，还有一个出口。

操作一系列指令让机器人一起上下左右走，走出矩形就死，进入出口则得救。

最多救多少机器人？

$W,H \leq 100$

考虑不让所有机器人移动，而让出口和矩形边界上下左右移动。

我们推一推性质。

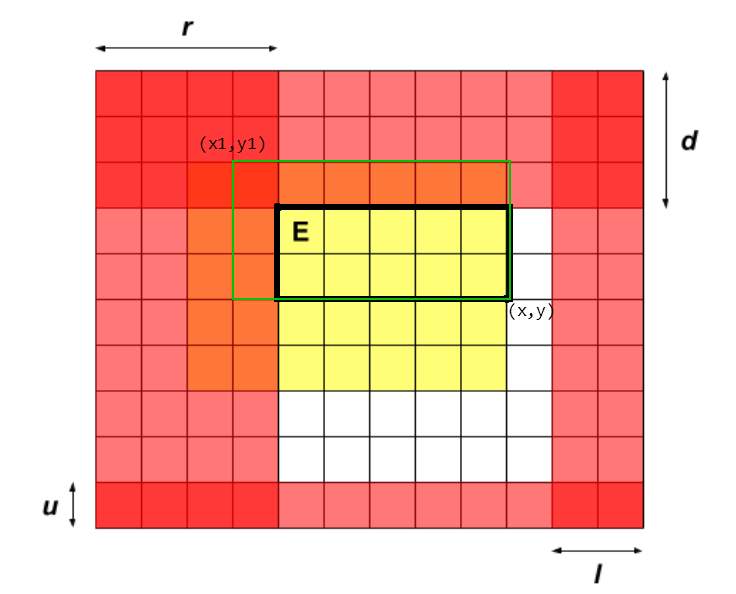
出口移动在一个矩形范围内(黄色矩形)的时候，会出边界的机器人是周围的一圈(红色部分)。

假如我们走到一个点$(x,y)$，如图，那么我们再走黑色框出来的矩形里面的地方，是不会让其它没死的机器人出边界的。

如果我们不仅走到了$(x,y)$，还走到过$(x1,y1)$，那么我们再走绿色框出来的矩形里面的地方，是不会让其它没死的机器人出边界的。

这些性质让我们大受启发，我们考虑$dp[xl][xr][yl][yr]$，表示我现在走出来的矩形是$[(xl,xr),(yl,yr)]$的最优解。

然后每次可以多加一行或者一列转移。

空间有点卡，可以用short。