绑定

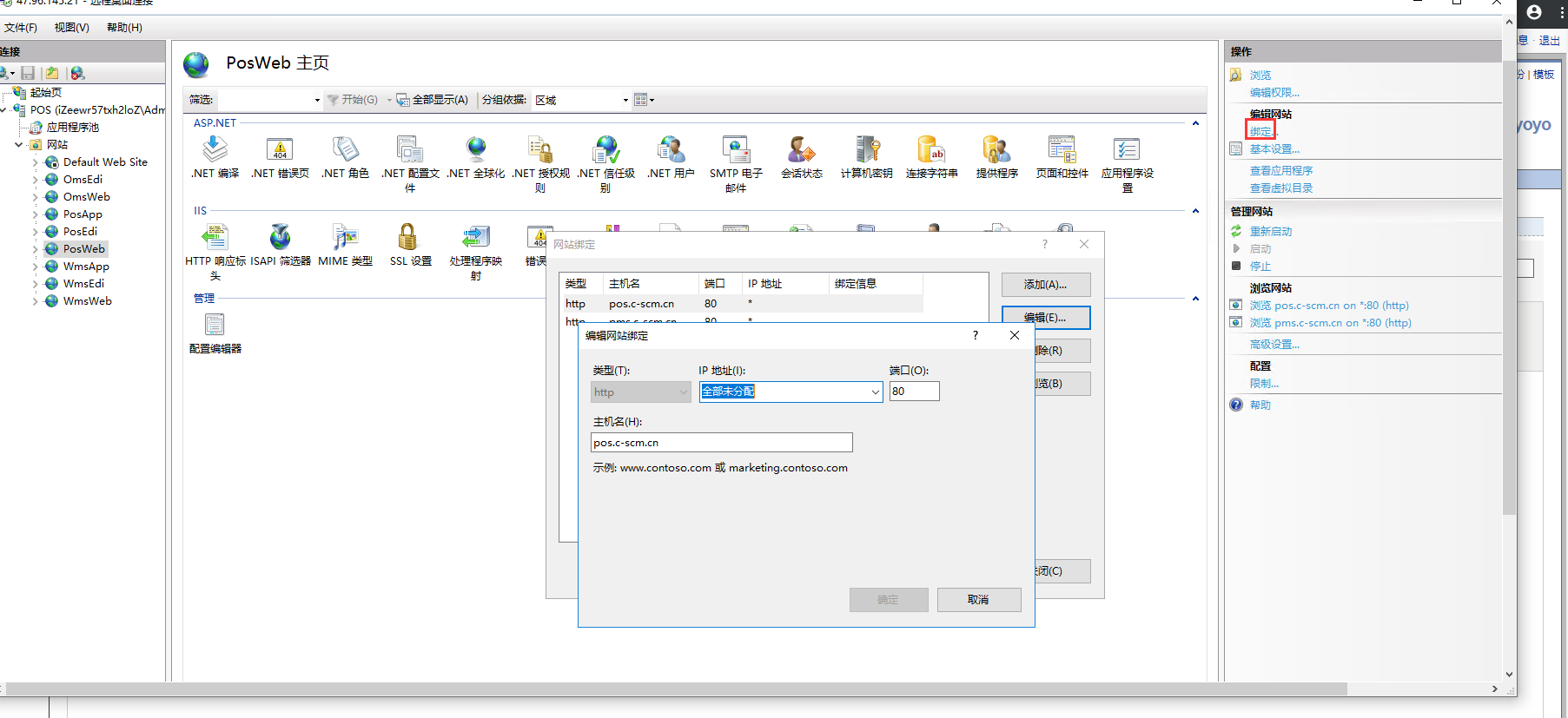
基本配置

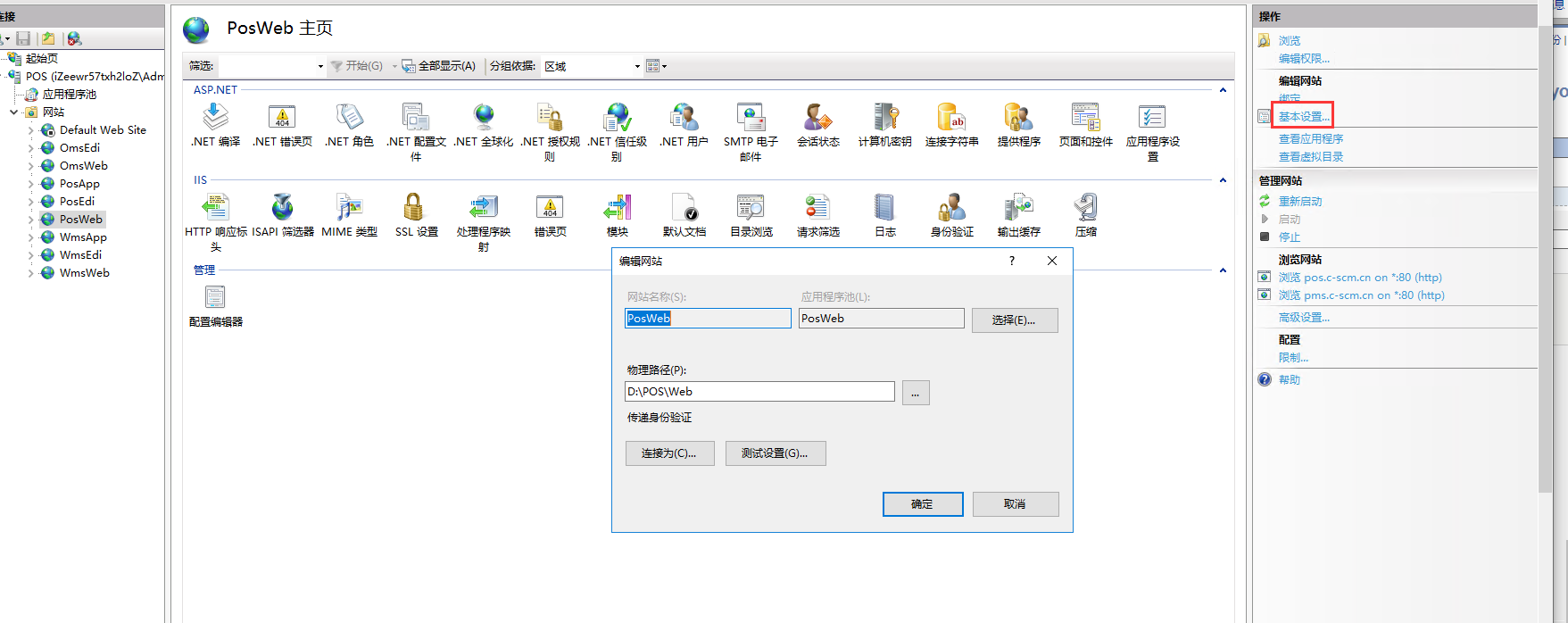
高级配置

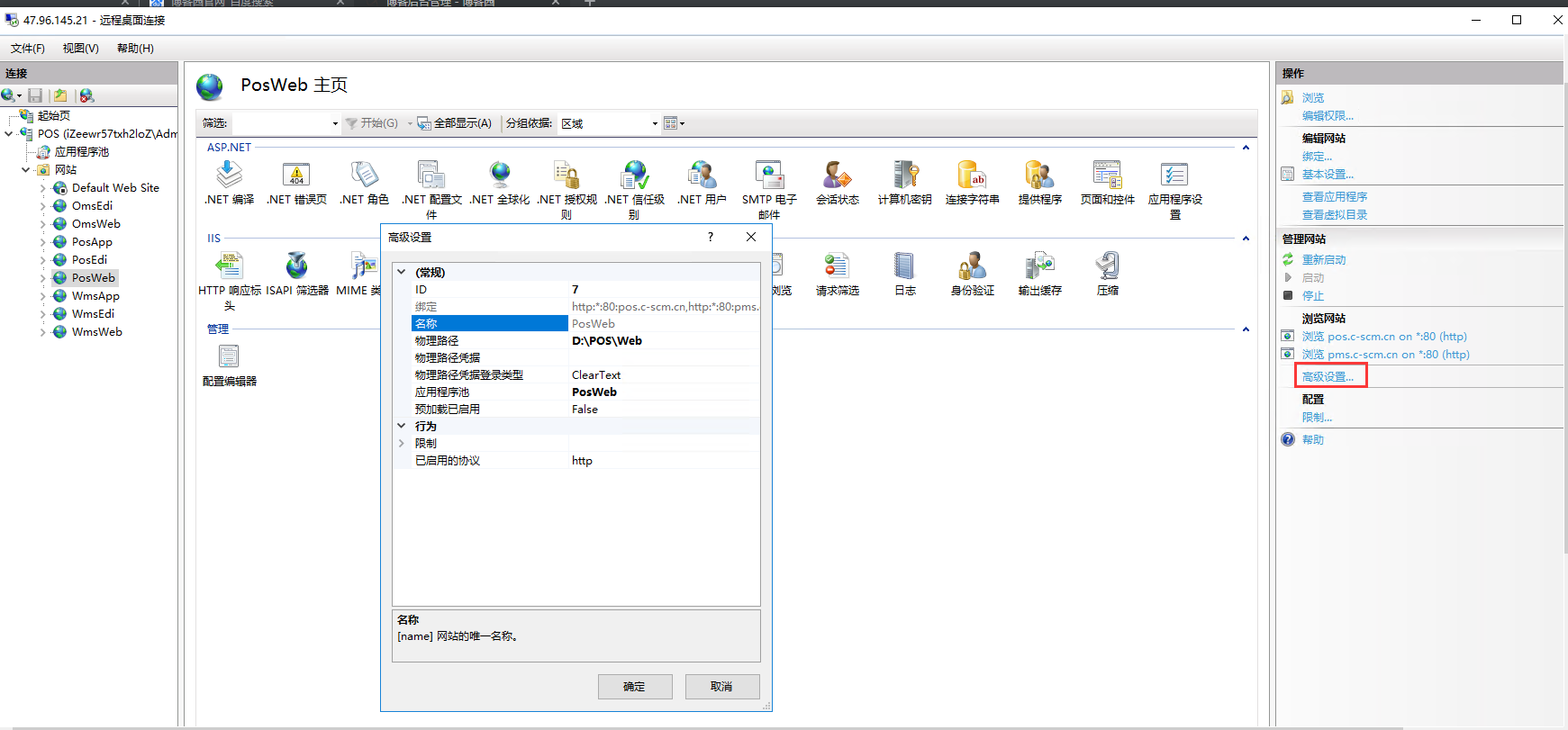
服务器迁移部署PosWeb的更多相关文章

  1. 服务器迁移部署PosEdi

    绑定 基本配置 高级配置

  2. 服务器迁移部署PosApp

    绑定 基本配置 高级设置

  3. 服务器迁移部署OmsWeb

    绑定 基本设置 高级设置

  4. 服务器迁移部署OmsEdi

    基本配置 绑定 高级设置

  5. gitlab服务器迁移

    公司更换了新的服务器,需要把原先的gitlab迁移到新的服务器上. 1.迁移准备工作和思路:从a服务器迁移到b服务器,由于Gitlab自身的兼容性问题,高版本的Gitlab无法恢复低版本备份的数据,需 ...

  6. VMware vSphere6.0 服务器虚拟化部署安装图解

    一 VMware vSphere部署的前期规划要点 1 vSphere的优点 (略) 2 如何利用现在的设备架构虚拟化环境 在虚拟化过程中,用户大多会考虑目前现有的服务器.存储.交换机等基础设备是否可 ...

  7. VMware vSphere6.0 服务器虚拟化部署安装图解(最全，最详细)-搭建的所有步骤

    VMware vSphere6.0 服务器虚拟化部署安装图解 一 .VMware vSphere部署的前期规划要点 1.vSphere的优点 (略) 2如何利用现在的设备架构虚拟化环境 在虚拟化过程中 ...

  8. Django项目在Linux服务器上部署和躺过的坑

    引言 在各方的推荐下,领导让我在测试环境部署之前开发的测试数据预报平台.那么问题来了,既然要在服务器上部署, 就需要准备: 1.linux服务器配置 2.linux安装python环境搭建与配置 3. ...

  9. Oracle 服务器迁移的一些经验

    前言 通过此文章来分享一下 Oracle 服务器迁移过程中的一些经验,希望对大家有些许帮助. 本文旨在帮助更多的同学,会提及一些基本命令或技巧,但不赘述,后续有机会再进一步分享各个细节. 背景 之前因 ...

随机推荐

  1. Lucene TFIDFSimilarity评分公式详解

    版权声明:本文为博主原创文章,遵循CC 4.0 by-sa版权协议,转载请附上原文出处链接和本声明. 本文链接:https://blog.csdn.net/zteny/article/details/ ...

  2. 数组模拟stack

    package com.cxy.springdataredis.data; import java.util.Scanner; public class StackDemo { public stat ...

  3. kerberos协议介绍

    一.kerberos认证过程: client向kerberos服务请求,希望获取访问server的权限.kerberos得到了这个消息,首先得判断client是否是可信赖的,也就是白名单黑名单的说法. ...

  4. OpenCV-Python Tutorials目录

    版本 3.4.6 1 Introduction to OpenCV OpenCV介绍Learn how to setup OpenCV-Python on your computer! 2 Gui F ...

  5. JS函数 函数的作用，可以写一次代码，然后反复地重用这个代码。

    什么是函数 函数的作用,可以写一次代码,然后反复地重用这个代码. 如:我们要完成多组数和的功能. var sum; sum = 3+2; alert(sum); sum=7+8 ; alert(sum ...

  6. python读文件判断是否已到EOF

    python读文件判断是否已到EOF,也即结尾,一般其它语言都是以EOF直接来判断的,比如 if ( fp.read(chunk_size) == EOF), 但python到结尾后是返回空字符串的, ...

  7. hdu多校第二场 1005 （hdu6595） Everything Is Generated In Equal Probability

    题意: 给定一个N,随机从[1,N]里产生一个n,然后随机产生一个n个数的全排列,求出n的逆序数对的数量,加到cnt里,然后随机地取出这个全排列中的一个非连续子序列(注意这个子序列可以是原序列),再求 ...

  8. type元类创建类的方法

    一.代码 class_name='car' dict_name={} bases=(object,) class_body=''' def __init__(self,name): self.name ...

  9. grunt是什么

    Grunt是什么? 博客分类: Grunt GruntJavascript  Grunt是一个自动化的项目构建工具.如果你需要重复的执行像压缩,编译,单元测试,代码检查以及打包发布的任务.那么你可以使 ...

  10. System.Web.Mvc.RouteAttribute.cs

    ylbtech-System.Web.Mvc.RouteAttribute.cs 1.程序集 System.Web.Mvc, Version=5.2.3.0, Culture=neutral, Pub ...