PP: UMAP: uniform manifold approximation and projection for dimension reduction

From Tutte institute for mathematics and computing

Problem: dimension reduction

Theoretical foundations:

At a high level, UMAP uses local manifold approximations and patches together their local fuzzy simplicial set representations to construct a topological representation of the high dimensional data. Given some low dimensional representation of the data, a similar process can be used to construct an equivalent topological representation. UMAP then optimizes the layout of the data representation in the low dimensional space, to minimize the cross-entropy between the two topological representations.

解释：使用local manifold approximations and local fuzzy simplicial set presentations, 在高维空间上构建了一个拓扑表征topological representation，在低维空间上，同样构建一个等价的拓扑表征，之后运用交叉熵作为优化函数，来计算两个空间拓扑表征的差异性，从而使差异性最小化。

Construction of fuzzy topological representations:

1. approximating a manifold on which the data is assumed to lie;

2. constructing a fuzzy simplicial set representation of the approximated manifold.

解释：

疑问：一组高维数据究竟落在哪？高维数据应该用哪个空间进行衡量？Euclidean space, topological space, Riemannian space还是啥空间测量？还是应用不同的空间策略都能得到相似的结果？

1. approximating a manifold on which the data is assumed to lie,

Suppose the manifold is not known in advance and we wish to approximate geodesic distance on it. Let the input data be X = {X1 , . . . , XN }.

A Computational view of UMAP:

Two phases.

In the first phase, a particular weighted k-neighbour graph is constructed. In the second phase, a low dimensional layout of this graph is computed

1. weighted k-neighbour graph construction

Use the nearest neighbor descent algorithm of [1]

2. low dimensional layout

Use force-directed graph layout in low dimensional space.

Implementation and hyper-parameters:

Supplementary knowledge:

1. simplicial sets. 单纯集

In mathematics, a simplicial set is an object made up of "simplices单纯形" in a specific way. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets and categories. 

simplex: 单纯形,

In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron四边形 to arbitrary dimensions.

For example,

• a 0-simplex is a point,
• a 1-simplex is a line segment,
• a 2-simplex is a triangle,
• a 3-simplex is a tetrahedron,
• a 4-simplex is a 5-cell.

2. Hadamard product/ pointwise product

3. What is n-skeleton?

4. mathematical conception

Convergent Sequence, 收敛序列

Space, space_conception_2,

The concept of a space is an extremely general and important mathematical construct. Members of the space obey certain addition properties. Spaces which have been investigated and found to be of interest are usually named after one or more of their investigators.

The everyday type of space familiar to most people is called Euclidean space. In Einstein's theory of Special Relativity, Euclidean three-space plus time (the "fourth dimension") are unified into the so-called Minkowski space. One of the most general type of mathematical spaces is the topological space.

Metric Space

A metric space is a set 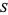 with a global distance function (the metric 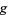) that, for every two points  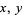in 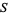, gives the distance between them as a nonnegative real number 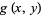. A metric space must also satisfy

1. 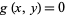 iff ,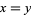

2. ,

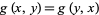3. The triangle inequality .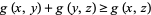

Euclidean space:

Euclidean 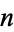-space, sometimes called Cartesian space or simply 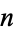-space, is the space of all n-tuples of real numbers, (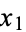, , 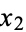..., 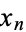). Such 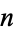-tuples are sometimes called points, although other nomenclature may be used (see below). The totality of 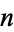-space is commonly denoted ,.

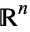Topological space:

A topological space, also called an abstract topological space, is a set 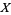 together with a collection of open subsets  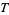that satisfies the four conditions:

1. The empty set 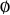 is in .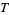

2. 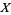 is in .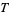

3. The intersection of a finite number of sets in 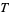 is also in .

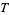4. The union of an arbitrary number of sets in 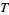 is also in .

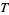 Triangle inequality

Let  and 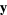 be vectors. Then the triangle inequality is given by

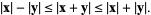(1)

Equivalently, for complex numbers 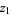 and ,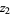

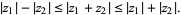5. the difference between Euclidean space and Riemannian space

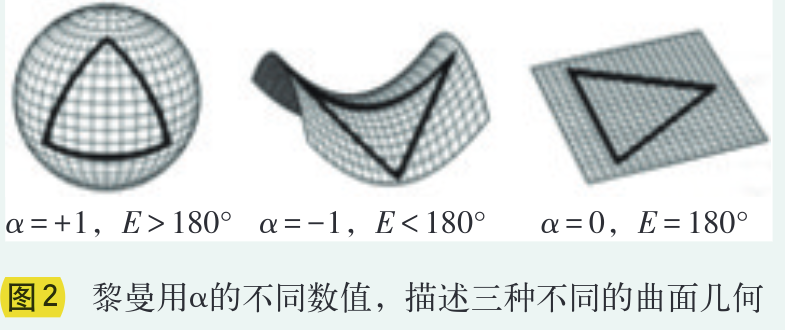
黎曼将二维曲面的球面几何、双曲几何(即罗巴切夫斯基几何)和欧氏几何统一在下述黎曼度规表达式中

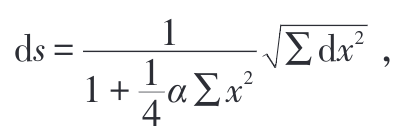
这个弧长微分ds表达式中的α，是2维曲面的高斯曲率。当α=+1时，度规所描述的是三角形内角和E大于180°的球面几何；当α=-1时，所描述的是内角和E小于180°的双曲几何；当α=0，则对应于通常的欧几里德几何(图2)。黎曼引入度规的概念，将三种几何统一在一起，使得非欧几何焕发出蓬勃的生机。

Reference

1. Efficient k-nearest neighbor graph construction for generic similarity measures

2. 欧氏空间与黎曼空间