leetcode-229-求众数②
题目描述:
方法一:摩尔投票法
class Solution:
def majorityElement(self, nums: List[int]) -> List[int]:
candiate1 = candiate2 = None
cnt1 = cnt2 = 0
for num in nums:
if num == candiate1:
cnt1 += 1
elif num == candiate2:
cnt2 += 1
elif cnt1 == 0:
candiate1 = num
cnt1 = 1
elif cnt2 == 0:
candiate2 = num
cnt2 = 1
else:
cnt1 -= 1
cnt2 -= 1
return [n for n in (candiate1, candiate2) if nums.count(n)>len(nums)//3]
附:169 求众数1
题目描述:
class Solution:
def majorityElement(self, nums):
count = 0
candidate = None for num in nums:
if count == 0:
candidate = num
count += (1 if num == candidate else -1) return candidate
leetcode-229-求众数②的更多相关文章
- Java实现 LeetCode 229 求众数 II(二)
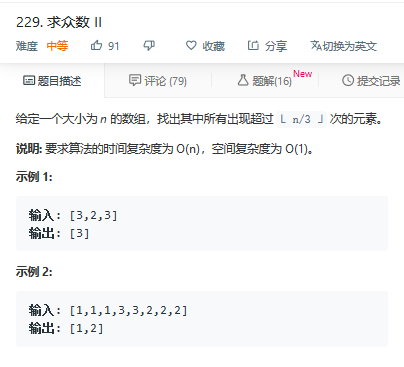
229. 求众数 II 给定一个大小为 n 的数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素. 说明: 要求算法的时间复杂度为 O(n),空间复杂度为 O(1). 示例 1: 输入: [3,2, ...
- Leetcode 229.求众数II
求众数II 给定一个大小为 n 的数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素. 说明: 要求算法的时间复杂度为 O(n),空间复杂度为 O(1). 示例 1: 输入: [3,2,3] 输出: ...
- LeetCode 229. 求众数 II(Majority Element II )
题目描述 给定一个大小为 n 的数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素. 说明: 要求算法的时间复杂度为 O(n),空间复杂度为 O(1). 示例 1: 输入: [3,2,3] 输出: ...
- 229. 求众数 II
Q: 给定一个大小为 n 的数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素. 说明: 要求算法的时间复杂度为 O(n),空间复杂度为 O(1). 示例 1: 输入: [3,2,3] 输出: [3 ...
- leetcode之求众数
求众数 给定一个大小为 n 的数组,找到其中的众数. 你可以假设数组是非空的,并且给定的数组总是存在众数. 示例 1: 输入: [3,2,3] 输出: 3 示例 2: 输入: [2,2,1,1,1,2 ...
- 面试之leetcode分治-求众数,x幂等
1 leetcode50 计算 x 的 n 次幂函数. 实现 pow(x, n) ,即计算 x 的 n 次幂函数. (1)调用库函数 (2)暴力o(N) (3)分治 xxxxxx.......x ...
- LeetCode(169. 求众数)
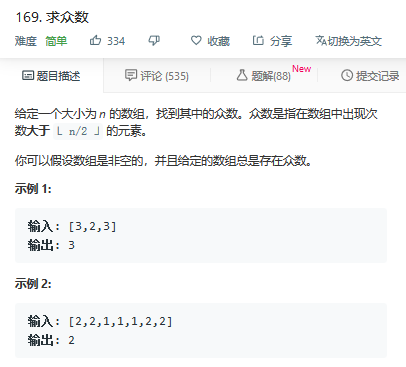
问题描述 给定一个大小为 n 的数组,找到其中的众数.众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素. 你可以假设数组是非空的,并且给定的数组总是存在众数. 示例 1: 输入: [3,2,3] ...
- 【LeetCode】求众数
给定一个大小为 n 的数组,找到其中的众数.众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素. 你可以假设数组是非空的,并且给定的数组总是存在众数. class Solution(object): ...
- 力扣(LeetCode)求众数 个人题解
给定一个大小为 n 的数组,找到其中的众数.众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素. 你可以假设数组是非空的,并且给定的数组总是存在众数. 示例 1: 输入: [3,2,3] 输出: 3 ...
- Java实现 Leetcode 169 求众数
public static int majorityElement(int[] nums) { int num = nums[0], count = 1; for(int i=1;i<nums. ...
随机推荐
- Array.prototype.slice.call()等几种将arguments对象转换成数组对象的方法
网站搬迁,给你带来的不便敬请谅解! http://www.suanliutudousi.com/2017/10/10/array-prototype-slice-call%E7%AD%89%E5%87 ...
- 【centos】 error: command 'gcc' failed with exit status 1 错误
转载自 :http://blog.csdn.net/fenglifeng1987/article/details/38057193 用安装Python模块出现error: command 'gcc' ...
- 数据转换--替换值(replace函数)
替换值 replace函数 data=Series([1,-999,2,-999,-1000,3]) data Out[34]: 0 1 1 -999 2 2 3 -999 4 -1000 5 3 d ...
- codeforces750E New Year and Old Subsequence 矩阵dp + 线段树
题目传送门 思路: 先看一个大牛的题解 题解里面对矩阵的构造已经写的很清楚了,其实就是因为在每个字符串都有固定的很多中状态,刚好可以用矩阵来表达,所以$(i,j)$这种状态可以通过两个相邻的矩阵的$m ...
- PushSharp 由于远程方已关闭传输流,身份验证失败。
前段时间用到了PushSharp给APNS发推送,但是用的时候遇见很诡异的事情,每次第一次运行的时候能成功发送到 但是接下来就无限的提示“由于远程方已关闭传输流,身份验证失败. “ 然后我就各种找原因 ...
- top.location.href
window.location.href.location.href是本页面跳转 parent.location.href是上一层页面跳转 top.location.href是最外层的页面跳转 ...
- kubeadm部署一个Kubernetes集群
kubeadm是官方社区推出的一个用于快速部署kubernetes集群的工具.这个工具能通过两条指令完成一个kubernetes集群的部署: # 创建一个 Master 节点 $ kubeadm in ...
- C中为什么不能用==比较字符串?
通常的回答是,==比较的不是字符串的内容,它是在比较指针.或者说,==(或者!=)仅比较两个字符串的首地址,而不会比较字符串每个字符. 那其实接下来应该问的问题是,为什么会只比较首地址呢? 因为早期的 ...
- Perl 哈希
Perl 哈希 哈希是 key/value 对的集合. Perl中哈希变量以百分号 (%) 标记开始. 访问哈希元素格式:${key}. 以下是一个简单的哈希实例: 实例 #!/usr/bin/per ...
- dvaJs使用注意事项
项目参考地址 dva-yicha 1. 使用路由跳转的方式 (1)所有的路由跳转功能都放到 dva/router 里面的 import { routerRedux } from 'dva/router ...
