Code Force 429B Working out【递推dp】

Summer is coming! It's time for Iahub and Iahubina to work out, as they both want to look hot at the beach. The gym where they go is a matrix a with n lines and mcolumns. Let number a[i][j] represents the calories burned by performing workout at the cell of gym in the i-th line and the j-th column.

Iahub starts with workout located at line 1 and column 1. He needs to finish with workout a[n][m]. After finishing workout a[i][j], he can go to workout a[i + 1][j] or a[i][j + 1]. Similarly, Iahubina starts with workout a[n][1] and she needs to finish with workout a[1][m]. After finishing workout from cell a[i][j], she goes to either a[i][j + 1] or a[i - 1][j].

There is one additional condition for their training. They have to meet in exactly one cell of gym. At that cell, none of them will work out. They will talk about fast exponentiation (pretty odd small talk) and then both of them will move to the next workout.

If a workout was done by either Iahub or Iahubina, it counts as total gain. Please plan a workout for Iahub and Iahubina such as total gain to be as big as possible. Note, that Iahub and Iahubina can perform workouts with different speed, so the number of cells that they use to reach meet cell may differs.

Input

The first line of the input contains two integers n and m (3 ≤ n, m ≤ 1000). Each of the next n lines contains m integers: j-th number from i-th line denotes element a[i][j] (0 ≤ a[i][j] ≤ 10⁵).

Output

The output contains a single number — the maximum total gain possible.

Example

Input

3 3
100 100 100
100 1 100
100 100 100

Output

800

Note

Iahub will choose exercises a[1][1] → a[1][2] → a[2][2] → a[3][2] → a[3][3]. Iahubina will choose exercises a[3][1] → a[2][1] → a[2][2] → a[2][3] → a[1][3].

题意：一个人从左上角走到右下角，另一个人从左下角走到右上角，格子上有数，求两个人得到的最大格子数之和为多少。两人只能在一个格子相遇，这个格子的值不计入最后结果。（当然，他们一个只能向下和向右走，另一个只能向上和向右走。）

我觉得这道题好棒!虽然不会。实在不知道这怎么dp。

我没有发现一个重要的性质：当两人相遇后，他们只能沿各自原来的方向走。

画个示意图：

　　

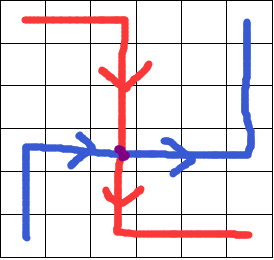
按照规则俩人相遇后只能按照原来的方向走才不会有多个交点，这就推出他们在边界不可能相遇。所以每次O((n-1)^2)的复杂度枚举交点，按四个方向递推dp求解。至于为什么要四个方向dp而不是两个，可以对照上图或者手动画一画想想。

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int MAXN = ;
 int dp1[MAXN][MAXN], dp2[MAXN][MAXN], dp3[MAXN][MAXN], dp4[MAXN][MAXN];
 int a[MAXN][MAXN];
 int ans;

 int max(int a, int b)
 {
     if (a < b) return b;
     return a;
 }

 int main()
 {
     int n, m;
     cin >> n >> m;
     for (int i = ; i <= n; i++)
         for (int j = ; j <= m; j++)
             cin >> a[i][j];
     for (int i = ; i <= n; i++)
         for (int j = ; j <= m; j++)
             dp1[i][j] = a[i][j] + max(dp1[i - ][j], dp1[i][j - ]);
     for (int i = n; i >= ; i--)
         for (int j = m; j >= ; j--)
             dp2[i][j] = a[i][j] + max(dp2[i + ][j], dp2[i][j + ]);
     for (int i = n; i >= ; i--)
         for (int j = ; j <= m; j++)
             dp3[i][j] = a[i][j] + max(dp3[i][j - ], dp3[i + ][j]);
     for (int i = ; i <= n; i++)
         for (int j = m; j >= ; j--)
             dp4[i][j] = a[i][j] + max(dp4[i - ][j], dp4[i][j + ]);
     ans = ;
     for (int i = ; i<n; i++)
         for (int j = ; j < m; j++) {
             ans = max(ans, dp1[i - ][j] + dp2[i + ][j] + dp3[i][j - ] + dp4[i][j + ]);
             ans = max(ans, dp1[i][j - ] + dp2[i][j + ] + dp3[i + ][j] + dp4[i - ][j]);
         }
     cout << ans << endl;
     return ;
 }

参考博客（感谢~）:

【1】：http://blog.csdn.net/qq_34374664/article/details/54577940

【2】：http://blog.csdn.net/tc_to_top/article/details/51875673