leetcode-回溯

题17：

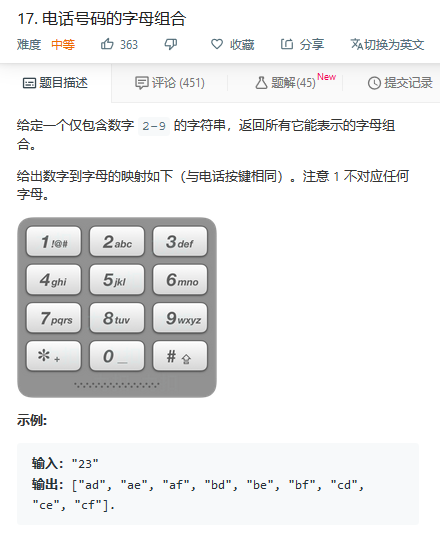
方法一：回溯

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        res = []
        dic ={"":"abc","":"def","":"ghi","":"jkl","":"mno","":"pqrs","":"tuv","":"wxyz"}
        def helper(s,ans):
            if not s:
                res.append(ans)
                return
            for i in dic[s[0]]:
                helper(s[1:],ans+i)
            ans = ans[:-1]

        if digits:helper(digits,"")
        return res

题22：

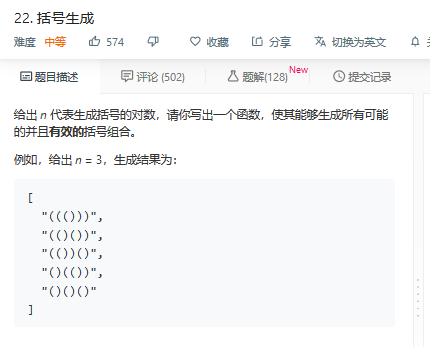
回溯：

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        res = []
        def helper(l,r,ans):
            if len(ans) == 2*n:
                res.append(ans)
                return
            if l<n:
                helper(l+1,r,ans+"(")
            if r<l:
                helper(l,r+1,ans+")")
        if n: helper(0,0,"")
        return res

题39：

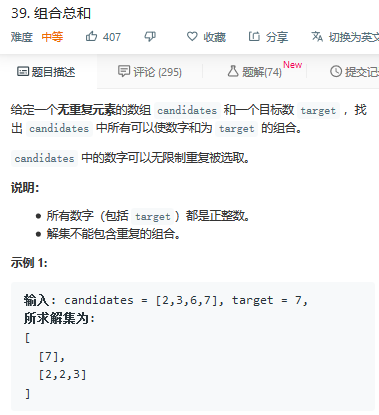
回溯：

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        res = []
        candidates.sort()
        def helper(c,t,ans):
            if t == 0:
                res.append(ans)
                return
            if t < 0:
                return
            for i,v in enumerate(c):
                if t - v < 0:
                    break
                helper(c[i:],t-v,ans+[v])
        if candidates:helper(candidates,target,[])
        return res

题40：

回溯：

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        res = []
        candidates.sort()
        def helper(c,t,ans):
            if t == 0:
                res.append(ans)
                return
            for i,v in enumerate(c):
                if t - v < 0:
                    break
                if i>0 and v == c[i-1]:continue
                else:
                    helper(c[i+1:],t-v,ans+[v])
        if candidates:helper(candidates,target,[])
        return res

题目46：

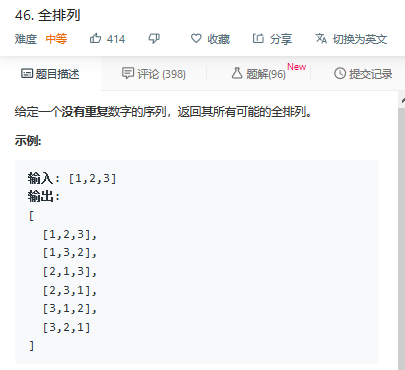
回溯：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []
        def helper(nums,ans):
            if not nums:
                res.append(ans)
                return
            for i in range(len(nums)):
                helper(nums[:i]+nums[i+1:],ans+[nums[i]])
        if nums:helper(nums,[])
        return res

题50：

回溯：

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        res = []
        visited = set()
        def helper(n,ans):
            if len(ans) == len(nums):
                res.append(ans)
                return
            for i in range(len(n)):
                if i in visited or (i>0 and i-1 not in visited and n[i]==n[i-1]):
                    continue
                visited.add(i)
                helper(n,ans+[n[i]])
                visited.remove(i)
        if nums:helper(nums,[])
        return res