nacos配置服务入门

1、nacos服务端部署
参见官方文档：https://nacos.io/zh-cn/docs/quick-start.html

2、nacos配置中心功能使用
在pol文件中添加依赖：

在启动类中使用@NacosPropertySources将配置引入到项目中
使用@NacosValue("${key}")获取配置指定配置
使用@Value("${key}")获取配置
使用ConfigService.getConfig()方法获取所有配置：
3、配置发布

@NacosInjected注解是nacos的一个核心注解，作用是在spring容器中注入ConfigService、NamingService等实例对象
注意：使用ConfigService.publishConfig方法发布配置会直接替换掉dataId下面的所有配置内容
4、配置修改监听
直接添加监听器

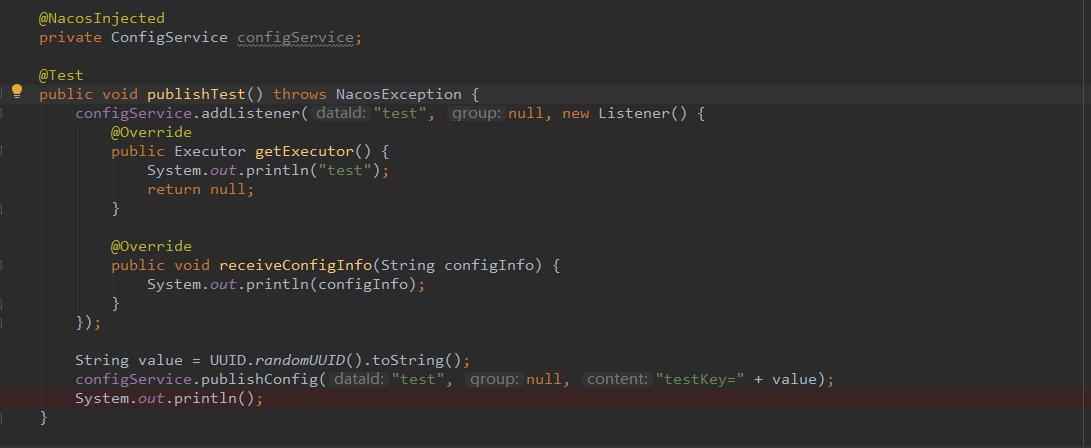
使用注解的方式添加：

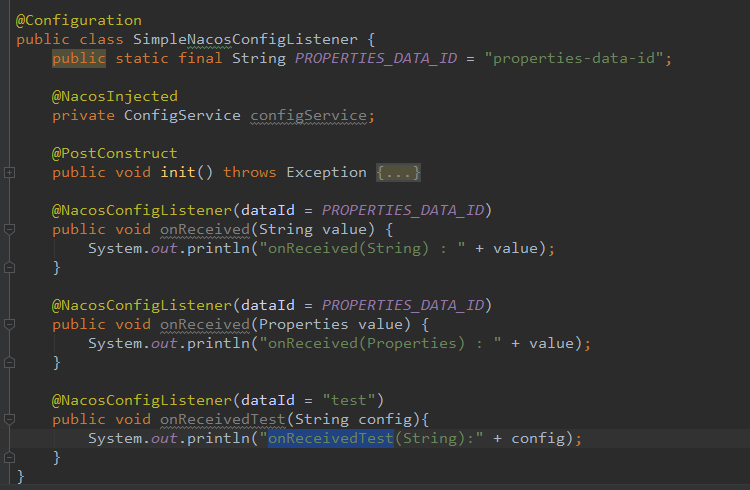
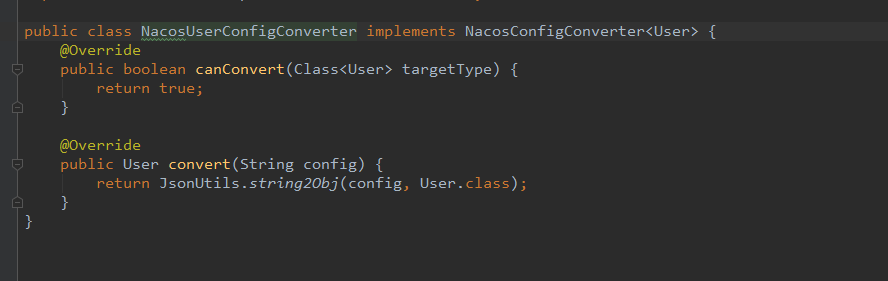
5、配置转换
自定义配置转换类，实现NacosConfigConverter接口

转换器使用

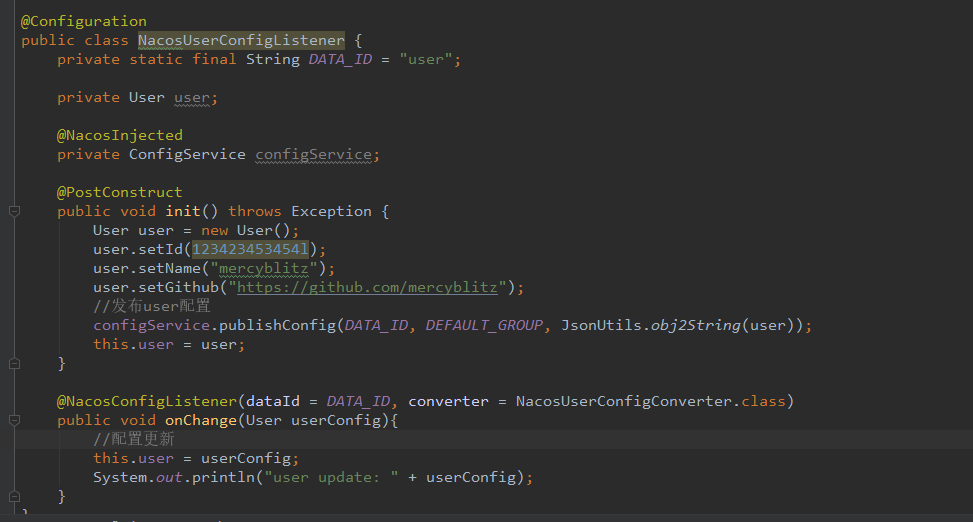
6、事件驱动
Nacos 事件驱动 基于标准的 Spring Event / Listener 机制

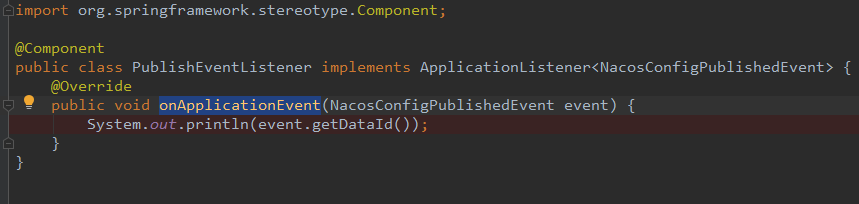
目前已知的Nacos支持的事件：

7、使用命名空间区分不同的环境配置
在配置文件中添加配置：
nacos.config.namespace =namespaceId