洛谷P3299 保护出题人

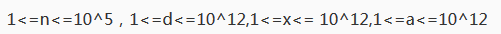
注意每一关的时候，前一关的植物会消失。保留整数指四舍五入。

解：冷静分析一波，列一个式子出来，发现每一关的植物攻击力要是(a_i + ... + a_j) / (x_i + d * (i - j))的最大值。1 <= j <= i

然后把这个东西写成前缀和，分母的i和j分离：(s_i - s_j-1) / (x_i + d * i - d * j))

发现就是两个点(x_i + d * i, s_i)和(d * j, s_j-1)之间的斜率。

于是维护一个下凸包然后凸包上三分就行了。注意到插入的点的横坐标单增，单调栈即可。

整数三分，就考虑l + 1 = r的时候怎么取，也比较好写。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;
 const double eps = 1e-;

 struct Vec {
     double x, y;
     Vec(double X = , double Y = ) {
         x = X;
         y = Y;
     }
     inline Vec operator + (const Vec &w) const {
         return Vec(x + w.x, y + w.y);
     }
     inline Vec operator - (const Vec &w) const {
         return Vec(x - w.x, y - w.y);
     }
     inline double operator * (const Vec &w) const {
         return x * w.y - y * w.x;
     }
 };
 typedef Vec Poi;

 Poi node[N];
 LL a[N], x[N], sum[N], d;
 int n, top, stk[N];

 int main() {
     scanf("%d%lld", &n, &d);
     for(int i = ; i <= n; i++) {
         scanf("%lld%lld", &a[i], &x[i]);
         sum[i] = sum[i - ] + a[i];
     }
     double ans = ;
     for(int i = ; i <= n; i++) {
         Poi now(x[i] + i * d, sum[i]);
         node[i] = Poi(i * d, sum[i - ]);
         while(top >  && (node[stk[top]] - node[stk[top - ]]) * (node[i] - node[stk[top]]) < eps) {
             top--;
         }
         stk[++top] = i;
         //printf("stk %d = %d (%lld %lld) \n", top, i, i * d, sum[i - 1]);
         //printf("now (%lld %lld) \n", x[i] + i * d, sum[i]);
         int l = , r = top;
         while(l < r) {
             int mid = (l + r) >> ;
             int ml = stk[mid], mr = stk[mid + ];
             double vl = (double)(sum[i] - sum[ml - ]) / (x[i] + (i - ml) * d),
                    vr = (double)(sum[i] - sum[mr - ]) / (x[i] + d * (i - mr));
             //printf("vl = %lf vr = %lf \n", vl, vr);
             //printf("x = %lld y = %lld = %lld + %d * %lld \n", sum[i], x[i] + i * d, x[i], i, d);
             if(vl < vr) {
                 l = mid + ;
             }
             else {
                 r = mid;
             }
         }
         ans += (double)(sum[i] - sum[stk[r] - ]) / (x[i] + (i - stk[r]) * d);
         //printf("ans += %lf \n", (double)(sum[i] - sum[stk[r] - 1]) / (x[i] + (i - stk[r]) * d));
         //printf("r = %d \n", r);
         /*for(int j = 1; j <= top; j++) {
             printf("%d ", stk[j]);
         }
         puts("");*/
     }

     printf("%.0f\n", ans);
     return ;
 }

AC代码