lasso-ridge

L1与L2正则化的区别与联系

L1正则化和L2正则化的说明如下：

L1正则化：\(\min _{w} \frac{1}{2 n_{\text {samples}}}\|X w-y\|_{2}^{2}+\alpha\|w\|_{1}\) 绝对值之和

L2正则化：\(\min _{w}\|X w-y\|_{2}^{2}+\alpha\|w\|_{2}^{2}\) 平方和

L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为||w||1

L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为||w||2

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择

L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

一般都会在正则化项之前添加一个系数，Python中用α表示，一些文章也用λ表示。这个系数需要用户指定。

L1  L2 区别：

相同点：都用于避免过拟合

不同点：L1可以让一部分特征的系数缩小到0，从而间接实现特征选择。所以L1适用于特征之间有关联的情况。

L2让所有特征的系数都缩小，但是不会减为0，它会使优化求解稳定快速。所以L2适用于特征之间没有关联的情况

1. L2 regularizer ：使得模型的解偏向于 norm 较小的 W，通过限制 W 的 norm 的大小实现了对模型空间的限制，从而在一定程度上避免了 overfitting 。不过 ridge regression 并不具有产生稀疏解的能力，得到的系数 仍然需要数据中的所有特征才能计算预测结果，从计算量上来说并没有得到改观。会选择更多的特征，这些特征都会接近于0。   最优的参数值很小概率出现在坐标轴上，因此每一维的参数都不会是0。当最小化||w||时，就会使每一项趋近于0
2. L1 regularizer ：** 它的优良性质是能产生稀疏性，因为最优的参数值很大概率出现在坐标轴上，这样就会导致某一维的权重为0 ，产生稀疏权重矩阵, 导致 W 中许多项变成零。** 稀疏的解除了计算量上的好处之外，更重要的是更具有“可解释性”csdn

L1稀疏性的原因

解空间形状直观理解

带正则项，相当于为目标函数的解空间进行了约束。当参数为2维时，为对于L2正则项，解空间为原型，L1正则项解空间为菱形。最优解必定是有且仅有一个交点。除非目标函数具有特殊的形状，否则和菱形的唯一交点大概率出现在截距处（即对应某一维度参数为0）。而对于圆形的解空间，总存在一个切点，且仅当某些特殊情况下，切点才会位于坐标轴上csdn

而正则化前面的系数α，可以控制L图形的大小。α越小，L的图形越大（上图中的黑色方框）；α越大，L的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。

类似，假设有如下带L2正则化的损失函数：

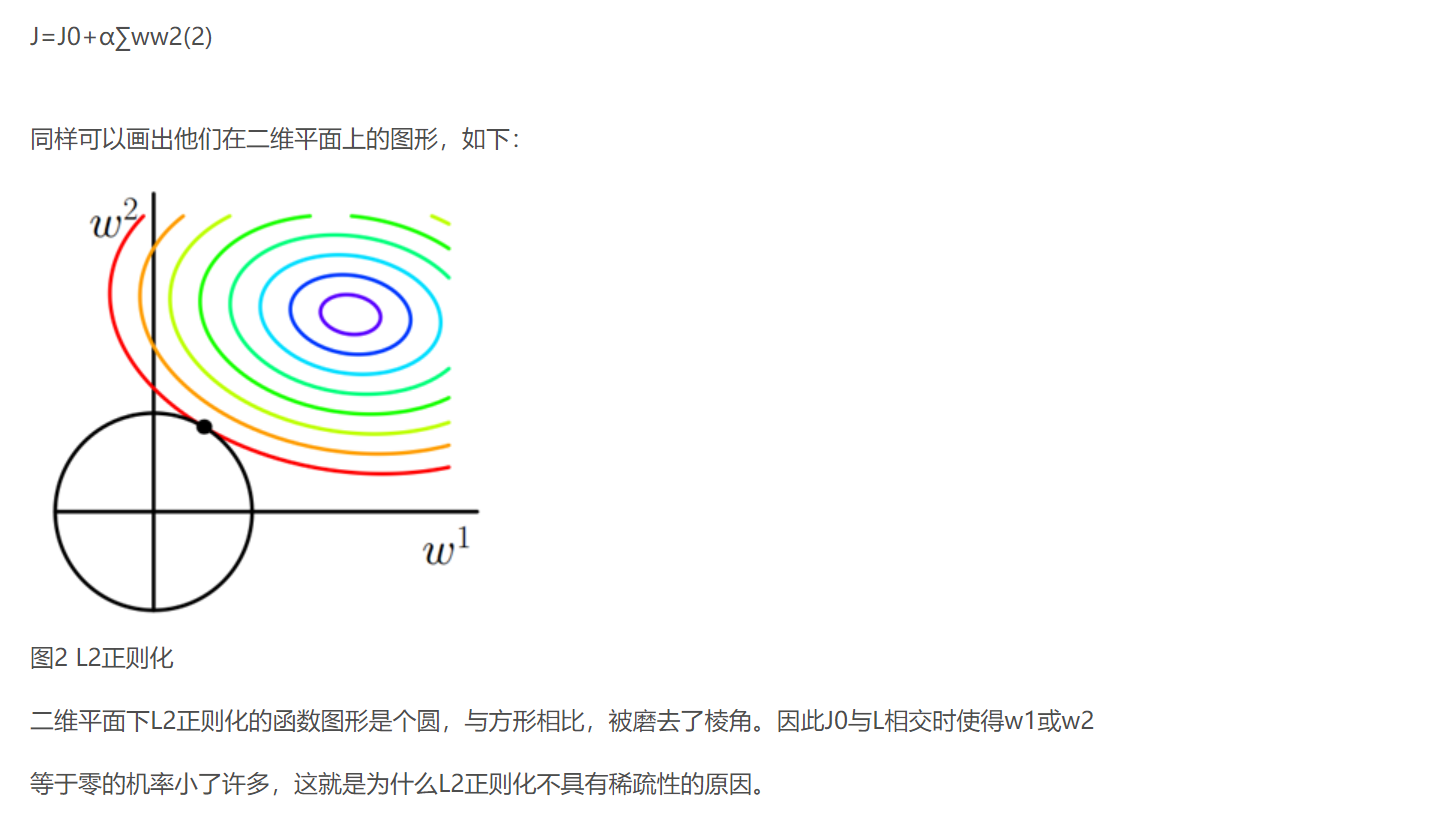
lasso 回归和岭回归（ridge regression）其实就是在标准线性回归的基础上分别加入 L1 和 L2 正则化（regularization）。

正则化

岭回归-Ridge

Loss function = OLS loss function +\(\alpha * \sum_{i=1}^{n} a_{i}^{2}\)

Lasso is great for feature selection, but when building regression models, Ridge regression should be your first choice.

datacamp

# Import necessary modules
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score

# Setup the array of alphas and lists to store scores
alpha_space = np.logspace(-4, 0, 50)
ridge_scores = []
ridge_scores_std = []

# Create a ridge regressor: ridge
ridge = Ridge(normalize=True)

# Compute scores over range of alphas
# 给出很多a值，调参，就是超参数调参
for alpha in alpha_space:

    # Specify the alpha value to use: ridge.alpha
    ridge.alpha = alpha

    # Perform 10-fold CV: ridge_cv_scores
    # 用到了10折交叉验证进行的调参
    ridge_cv_scores = cross_val_score(ridge, X, y, cv=10)

    # Append the mean of ridge_cv_scores to ridge_scores
    ridge_scores.append(np.mean(ridge_cv_scores))

    # Append the std of ridge_cv_scores to ridge_scores_std
    ridge_scores_std.append(np.std(ridge_cv_scores))

# Display the plot
display_plot(ridge_scores, ridge_scores_std)

Lasso_套索回归（最小绝对值收敛）

Loss function = OLS loss function +\(\alpha * \sum_{i=1}^{n}\left|a_{i}\right|\)

lasso一般用来进行特征选择

• hrinks the coefcients of less important features to exactly 0

# Import Lasso
from sklearn.linear_model import Lasso

# Instantiate a lasso regressor: lasso
lasso = Lasso(alpha=0.4, normalize=True)

# Fit the regressor to the data
lasso.fit(X, y)

# Compute and print the coefficients
lasso_coef = lasso.coef_
print(lasso_coef)

# Plot the coefficients
plt.plot(range(len(df_columns)), lasso_coef)
plt.xticks(range(len(df_columns)), df_columns.values, rotation=60)
plt.margins(0.02)
plt.show()