「CodeChef Dec13 REALSET」 Petya and Sequence 循环卷积

题目大意：

　　传送门

　　T组询问。

　　每组给一个数组，询问该数组是否循环移位线性无关，输出YES或NO。

题解：

　　LCA冬令营有讲……然而当时……

　　并不知道如何计算一个数组是否循环移位线性无关……网上也没有……学校还加了白名单，翻不了墙，看不了wiki（英文看不懂……）。所以这就是我怂题解的理由23333。

　　题解上说wiki上循环矩阵的行列式等于其DFT后点值乘积。即对于矩阵：

　　

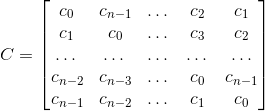
　　有：

　　

　　显然如果循环数组的矩阵的轶不为n的话其行列式必然为0。

　　所以把数组DFT以后看一下其乘积是否为0即可。

　　证明什么的……留个坑吧。

　　看到了一个大神打了几十行……没看懂在干什么……

　　LCA说还可以用分圆多项式，然而并没有找到资料。再留个坑吧……

代码：

 #include "bits/stdc++.h"

 using std::swap;

 inline int read () {
     int s=,k=;char ch=getchar();
     while (ch<''|ch>'') ch=='-'?k=-:,ch=getchar();
     while (ch>&ch<='') s=s*+(ch^),ch=getchar();
     return s*k;
 }

 typedef long long ll;

 const int N=1e5+;

 ll mod,g,w[][N],W[][N],n,m;

 inline ll gcd (ll a,ll b) {
     return b?gcd(b,a%b):a;
 }

 inline ll Mult ( ll a,ll b ) {
     return ( a*b - (ll)( (long double) a*b/mod )*mod + mod )% mod;
 }

 inline ll powmod ( ll a, ll b ) {
     ll ret=;
     while (b) {
         if (b&) ret=Mult ( ret, a );
         b>>=,a=Mult ( a, a);
     }return ret;
 }

 inline int is_prim(ll x) {
     for (int i=;1ll*i*i<=x;++i)
         if (x%i==) return false;
     return true;
 }

 inline int is_prim_root(ll x,ll y){
     for (int i=;1ll*i*i<y;++i)
         if ((y-)%i==) {
             if (powmod(x,i)==) return false;
             if (powmod(x,(y-)/i)==)return false;
         }
     return true;
 }

 inline void init () {
     for (m=;m<=*n;m<<=);
     ll lcm = n*m/gcd(n,m);
     mod = lcm + ;
     for (int i=;~i;--i)
         if (mod + (lcm<<i)<1e3*n) mod+=lcm<<i;
     while (mod<1e3*n) mod+=lcm;
     while (!is_prim(mod))  mod+=lcm;
     for (g=;;++g) {
         int flag=true;
         for (int i=;1ll*i*i<=mod;++i) if ((mod-)%i==){
             if (powmod(g,i)==) {flag=false;break;}
             if (powmod(g,(mod-)/i)==) {flag=false;break;}
         }
         if (flag) break;
     }

     ll w0=powmod(g,(mod-)/m);
     w[][]=w[][]=;
     int i;
     for (i=;i<m;++i) w[][i]=Mult(w[][i-],w0);
     for (i=;i<m;++i) w[][i]=w[][m-i];
     w0=powmod(g,(mod-)/n);
     W[][]=W[][]=;
     for (i=;i<n;++i) W[][i]=Mult(W[][i-],w0);
     for (i=;i<n;++i) W[][i]=W[][n-i];
 }

 inline void NTT(ll *a,int n,int f) {
     register int i,j,k,l,t;
     for (i=j=;i^n;++i) {
         if (i>j) std::swap(a[i],a[j]);
         for (k=n>>;(j^=k)<k;k>>=);
     }
     for (i=;i<n;i<<=)
         for (j=,t=n/(i<<);j<n;j+=i<<)
             for (k=l=;k<i;++k , l+=t ) {
                 ll x=a[j+k],y=Mult(a[i+j+k],w[f][l]);
                 a[j+k]=x+y;
                 a[i+j+k]=x-y;
                 if (a[j+k]>=mod) a[j+k]-=mod;
                 if (a[i+j+k]<) a[i+j+k]+=mod;
             }
     if (f ) {
         ll rev=powmod ( n,mod- );
         for (i=;i<n;++i) a[i]=Mult(a[i],rev);
     }
 }

 inline void Bluesteins(ll *a,int f){
     static ll X[N],Y[N];
     register int i;
     for (i=;i<*n;++i) Y[*n--i]=W[f][1ll*i*(i-)/%n];
     for (i=*n;i<m;++i) Y[i]=;
     NTT(Y,m,);
     for (i=;i<n;++i) X[i]=Mult(a[i],W[f][ (n-1ll*i*(i-)/%n)%n ]);
     for (i=n;i<m;++i) X[i]=;
     NTT(X,m,);
     for (i=;i<m;++i) X[i]=Mult(X[i],Y[i]);
     NTT(X,m,);
     for (i=;i<n;++i)
         a[i]=Mult (X[*n--i],W[f][(n-1ll*i*(i-)/%n)%n ]);
     if (f)  {
         ll rev=powmod(n,mod-);
         for (i=;i<n;++i) a[i]=Mult(a[i],rev);
     }
 }

 ll a[N];

 int main (int argc, char const* argv[]){
     //freopen("Dec13Realset.in","r",stdin);
     int T=read(),i;
     while (T-- ){
         n=read();
         for (i=;i<n;++i) a[i]=read();
         init();
         Bluesteins(a,);
         ll flag=;
         for (i=;i<n;++i) flag=Mult(flag,a[i]);
         puts(flag?"NO":"YES");
     }
     return ;
 }