FZU 1759 欧拉函数 降幂公式

Description

 

Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).

Input

There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.

Output

For each testcase, output an integer, denotes the result of A^B mod C.

Sample Input

3 2 4
2 10 1000

Sample Output

1
24

Hint

 

Source

FZU 2009 Summer Training IV--Number Theory

 

题意：A^B mod C

题解：

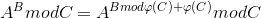
降幂公式 phi() 为欧拉函数

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #define ll __int64
 #define mod 10000000007
 using namespace std;
 char a[];
 ll x,z;
 ll quickpow(ll x,ll y,ll z)
 {
     ll ans=;
     while(y)
     {
         if(y&)
             ans=ans*x%z;
         x=x*x%z;
         y>>=;
     }
     return ans;
 }
 ll phi(ll n)
 {
     ll i,rea=n;
     for(i=;i*i<=n;i++)
     {
         if(n%i==)
         {
             rea=rea-rea/i;
             while(n%i==)
                 n/=i;
          }
     }
     if(n>)
         rea=rea-rea/n;
     return rea;
 }
 int main()
 {
     while(scanf("%I64d %s %I64d",&x,a,&z)!=EOF)
     {
         ll len=strlen(a);
         ll p=phi(z);
         ll ans=;
         for(ll i=;i<len;i++)
             ans=(ans*+a[i]-'')%p;
         ans+=p;
         printf("%I64d\n",quickpow(x,ans,z));
     }
     return ;
 }