poj 2195 Going Home

 /*
    做网络流的题建图真的是太重要了！
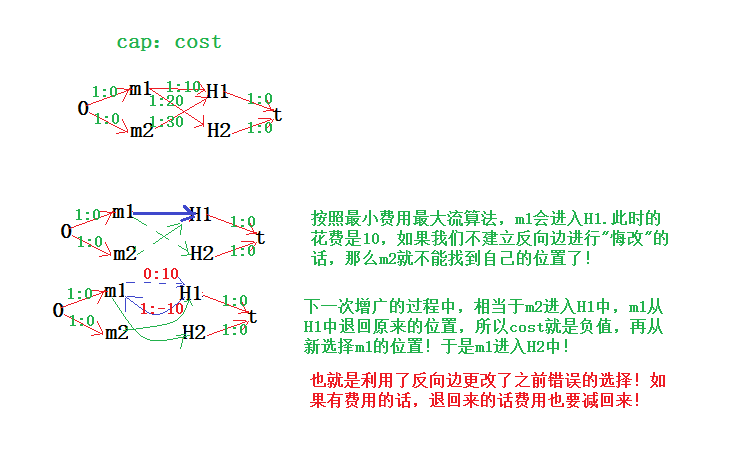
    本题是将人所在的位置和房子所在的位置建立边的联系，其中man到house这一条边的流量为 1， 费用为两者的距离
    而方向边的流量为 0， 费用为正向边的相反数（也就是沿着反向边进行增广时，费用要减少，更改先前错误的选择）
    最后增加一个源点和一个汇点完毕（源点映射到man， house映射到汇点， 费用为0， 流量为1） 
　　　　
 */
 #include<iostream>
 #include<cmath>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 #define Max 0x3f3f3f3f
 #define N 205
 using namespace std;

 class node
 {
 public:
    int x, y;
 };

 node xyM[N];
 node xyH[N];
 int cost[N][N], cap[N][N];
 int cntM, cntH;
 int pre[N*], dist[N*], vis[N*], n, m;

 void addE(int i, int j, int ct, int cp)
 {
     cost[i][j]=ct;
     cap[i][j]=cp;
     cost[j][i]=-ct;
     //cap[j][i]=0;
 }

 int s, t, minCost;

 void buildMap()
 {
    int i, j;
    memset(cap, , sizeof(cap));
    s=; t=cntM+cntH+;
    for(i=; i<cntM; ++i)
      addE(, i+, , );
    for(i=; i<cntH; ++i)
      addE(cntM+i+, t, , );
    for(i=; i<cntM; ++i)
      for(j=; j<cntH; ++j)
        addE(i+, cntM+j+, abs(xyM[i].x-xyH[j].x)+abs(xyM[i].y-xyH[j].y), );
 }

 queue<int>q;

 int spfa()
 {
     int u, v;
     memset(dist, 0x3f, sizeof(dist));
     dist[]=;
     q.push();
     vis[]=;
     while(!q.empty())
     {
         u=q.front();
         q.pop();
         vis[u]=;
         for(v=; v<=t; ++v)
           if(cap[u][v]> && dist[v]>dist[u]+cost[u][v])
           {
               dist[v]=dist[u]+cost[u][v];
               pre[v]=u;
               if(!vis[v])
               {
                     vis[v]=;
                     q.push(v);
           }
       }
     }
     if(dist[t]==Max)
       return ;
     return ;
 }

 void updateEdge()
 {
    int u, minFlow=Max;
    for(u=t; u!=s; u=pre[u])//通过最短路径寻找这条路径上的最小流量
       if(cap[pre[u]][u]<minFlow)
         minFlow=cap[pre[u]][u];
     for(u=t; u!=s; u=pre[u])
     {
         cap[pre[u]][u]-=minFlow;
         cap[u][pre[u]]+=minFlow;
         minCost+=cost[pre[u]][u];
     }
 }

 int main()
 {
    int i, j;
    char c;
    while(scanf("%d%d", &n, &m) && (n||m))
    {
        cntM=cntH=;
        minCost=;
        for(i=; i<=n; ++i)
          {
            getchar();
        for(j=; j<=m; ++j)
              {
             scanf("%c", &c);
             if(c=='m')
             {
                xyM[cntM].x=i;
                xyM[cntM++].y=j;
         }
         else if(c=='H')
         {
            xyH[cntH].x=i;
                xyH[cntH++].y=j;
         }
          }
         }
         buildMap();
         while(spfa())
           updateEdge();
         printf("%d\n", minCost);
    }
    return ;
 }

//邻接表

 #include<iostream>
 #include<queue>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #define INF 0x3f3f3f3f
 #define N 1000005
 using namespace std;

 int cntH, cntM;

 struct node{
     int x, y;
 };

 struct EDGE{
     int u, v, cap, cost, nt;
 };
 EDGE edge[N];

 queue<int>q;
 node man[], house[];
 int first[];
 int dist[];
 int pre[], flow[], vis[];
 int cnt, t;
 int minCost;
 int n, m;

 void addEdge(int u, int v, int cap, int cost){
     edge[cnt].u=u;
     edge[cnt].v=v;
     edge[cnt].cap=cap;
     edge[cnt].nt=first[u];
     edge[cnt].cost=cost;
     first[u]=cnt++;

     edge[cnt].u=v;
     edge[cnt].v=u;
     edge[cnt].cap=;
     edge[cnt].nt=first[v];
     edge[cnt].cost=-cost;
     first[v]=cnt++;
 }

 void buildMap(){
     memset(first, -, sizeof(first));
     t=cntH+cntM+;
     for(int i=; i<=cntM; ++i)
         for(int j=; j<=cntH; ++j)
             addEdge(i, cntM+j, , abs(man[i].x-house[j].x) + abs(man[i].y-house[j].y));
     for(int i=; i<=cntM; ++i)
         addEdge(, i, , );
     for(int i=; i<=cntH; ++i)
         addEdge(cntM+i, t, , );
 }

 bool MCMF(){
     memset(dist, 0x3f, sizeof(dist));
     memset(vis, , sizeof(vis));
     q.push();
     flow[]=INF;
     dist[]=;
     vis[]=;
     while(!q.empty()){
         int u=q.front(); q.pop();
         vis[u]=;
         for(int e=first[u]; ~e; e=edge[e].nt){
             int v=edge[e].v, cap=edge[e].cap, cost=edge[e].cost;
             if(cap> && dist[v]>dist[u]+cost){
                 dist[v]=dist[u]+cost;
                 flow[v]=min(flow[u], cap);
                 pre[v]=e;
                 if(!vis[v]){
                     vis[v]=;
                     q.push(v);
                 }
             }
         }
     }
     if(dist[t]==INF) return false;
     minCost+=dist[t];
     int x=t;
     while(x!=){
         edge[pre[x]].cap-=flow[t];
         edge[pre[x]^].cap+=flow[t];
         x=edge[pre[x]].u;
     }
     return true;
 }

 int main(){
     while(scanf("%d%d", &n, &m) && (n||m)){
         cnt=cntH=cntM=;
         for(int i=; i<=n; ++i){
             getchar();
             for(int j=; j<=m; ++j){
                 char ch;
                 scanf("%c", &ch);
                 if(ch=='m'){
                     man[++cntM].x=i;
                     man[cntM].y=j;
                 }
                 else if(ch=='H'){
                     house[++cntH].x=i;
                     house[cntH].y=j;
                 }
             }
         }
         buildMap();
         minCost=;
         while(MCMF());
         printf("%d\n", minCost);
     }
     return ;
 }