[原][数学][C++][osg]空间向量OA到转到空间向量OB、以及四元素Q1转到Q2的函数

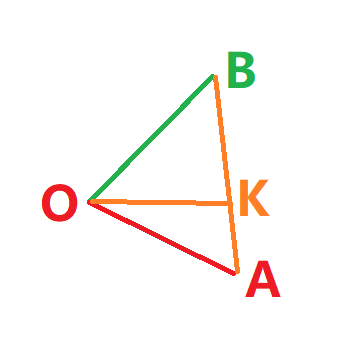
注意：Oa其实在OK的延长线上，上图只是为了好看才把Oa和OK分开了

算法需求如图所示：

已知空间向量OA和空间向量OB

我想算出OA向OB按某角度或者某时间移动

变成空间向量Oa的算法

先说废话：我一开始尝试了：空间平面、矩阵、四元素等等方式都能算出来，但是很繁琐。

然后发现，其实向量之间的算法完全能满足需求：

1.先求出向量AB

2.然后按某时间，某角度或者某百分比 乘以AB向量得到向量：AK

3.OA+AK=OK

4.将OK的向量归一化，乘以OA的模（长度）得到Oa

注意：Oa其实在OK的延长线上，上图只是为了好看才把Oa和OK分开了

 osg::Vec3d rotateVector(double time, osg::Vec3d OA, osg::Vec3d OB)
 {
     //http://www.cnblogs.com/lyggqm/p/8820676.html
     osg::Vec3d _Oa;
     osg::Vec3d AB = OB - OA;
     if (time >=0.0 && time <= 1.0)
         AB *= time;//AK = AB*time
     else
         return OA;
     osg::Vec3d OK = OA + AB;
     OK.normalize();//因为OA,OB传入的已经是normalize的所以OK就是Oa了
     _Oa = OK;
     return _Oa;
 }

算法结束

由此算法，再给出一个osg空间四元素q1转到空间四元素q2的函数吧：（与之前算法无关）

 /// Spherical Linear Interpolation
 /// As t goes from 0 to 1, the Quat object goes from "from" to "to"
 /// Reference: Shoemake at SIGGRAPH 89
 /// See also
 /// http://www.gamasutra.com/features/programming/19980703/quaternions_01.htm
 void Quat::slerp( value_type t, const Quat& from, const Quat& to )
 {
     const double epsilon = 0.00001;
     double omega, cosomega, sinomega, scale_from, scale_to ;
 
     osg::Quat quatTo(to);
     // this is a dot product
 
     cosomega = from.asVec4() * to.asVec4();
 
     if ( cosomega <0.0 )
     {
         cosomega = -cosomega;
         quatTo = -to;
     }
 
     if( (1.0 - cosomega) > epsilon )
     {
         omega= acos(cosomega) ;  // 0 <= omega <= Pi (see man acos)
         sinomega = sin(omega) ;  // this sinomega should always be +ve so
         // could try sinomega=sqrt(1-cosomega*cosomega) to avoid a sin()?
         scale_from = sin((1.0-t)*omega)/sinomega ;
         scale_to = sin(t*omega)/sinomega ;
     }
     else
     {
         /* --------------------------------------------------
            The ends of the vectors are very close
            we can use simple linear interpolation - no need
            to worry about the "spherical" interpolation
            -------------------------------------------------- */
         scale_from = 1.0 - t ;
         scale_to = t ;
     }
 
     *this = (from*scale_from) + (quatTo*scale_to);
 
     // so that we get a Vec4
 }
 
 //*************以下是用法*******************/
 
 osg::Quat    q1,q2;
 double time;//time是0到1值
 //.......赋值不表
 
 q1.slerp(time, q1, q2);//q1按time百分比转到q2