cdqz2017-test10-加帕里图书馆（区间DP & 简单容斥）

给定一个由小写字母组成的字符串，输出有多少重复的回文子序列

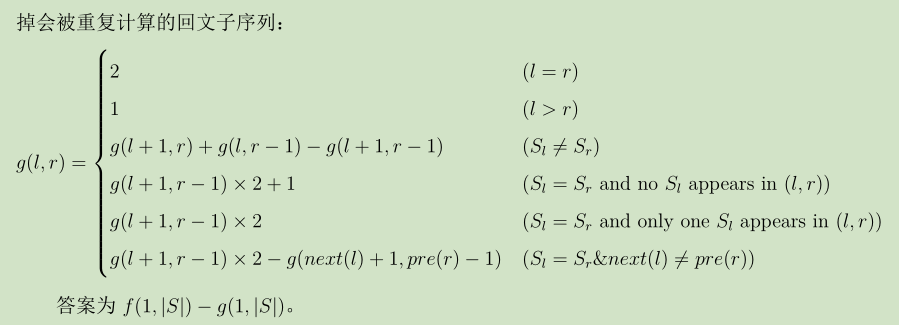
#include<cstdio>
#include<cstring>

using namespace std;

#define N 2002

const int mod=1e9+;

int n;
char s[N];

int f[N][N],g[N][N];

int pre[N][],nxt[N][];

int get_f(int l,int r)
{
    if(l>r) return ;
    int &ans=f[l][r];
    if(ans!=-) return ans;
    if(s[l]==s[r]) ans=get_f(l+,r)+get_f(l,r-);
    else ans=get_f(l+,r)+get_f(l,r-)-get_f(l+,r-);
    ans%=mod;
    if(ans<) ans+=mod;
    return ans;
}

int get_g(int l,int r)
{
    if(l==r) return ;
    if(l>r) return ;
    int &ans=g[l][r];
    if(ans!=-) return ans;
    if(s[l]!=s[r]) ans=get_g(l+,r)+get_g(l,r-)-get_g(l+,r-);
    else
    {
        if(nxt[l][s[l]-'a']>=r && pre[r][s[r]-'a']<=l) ans=get_g(l+,r-)*+;
        else if(nxt[l][s[l]-'a']==pre[r][s[r]-'a']) ans=get_g(l+,r-)*;
        else ans=get_g(l+,r-)*-get_g(nxt[l][s[l]-'a']+,pre[r][s[r]-'a']-);
    }
    ans%=mod;
    if(ans<) ans+=mod;
    return ans;
}

void cal()
{
    for(int i=;i<=n;++i)
    {
        for(int j=i+;j<=n;++j)
            if(!nxt[i][s[j]-'a']) nxt[i][s[j]-'a']=j;
        for(int j=i-;j;--j)
            if(!pre[i][s[j]-'a']) pre[i][s[j]-'a']=j;
    }
}

int main()
{
    freopen("library.in","r",stdin);
    freopen("library.out","w",stdout);
    scanf("%s",s+);
    n=strlen(s+);
    memset(f,-,sizeof(f));
    int all=get_f(,n);
    cal();
    memset(g,-,sizeof(g));
    int dif=get_g(,n);
    int ans=all-dif;
    if(ans<) ans+=mod;
    printf("%d",ans);
}

爆搜代码

#include<cstdio>
#include<cstring>

using namespace std;

int n;
char s[];

char tt[],t[];
int L;

int ans,sum;

int cnt[];

void find(int now,int len,int ok)
{
    if(ok==len)
    {
        sum++;
        return;
    }
    for(int i=now+;i<=n;++i)
        if(t[ok+]==s[i]) find(i,len,ok+);
}

void dfs(int len)
{
    for(int i=;i<;++i)
    {
        tt[len]=char(i+'a');
        L=;
        for(int j=len;j;--j) t[++L]=tt[j];
        for(int j=;j<=len;++j) t[++L]=tt[j];
        sum=;
        find(,L,);
        if(sum>) ans+=sum-;
        if(sum) dfs(len+);
    }
}

void dfs2(int len)
{
    for(int i=;i<;++i)
    {
        tt[len]=char(i+'a');
        L=;
        for(int j=len;j;--j) t[++L]=tt[j];
        for(int j=;j<=len;++j) t[++L]=tt[j];
        sum=;
        find(,L,);
        if(sum>) ans+=sum-;
        if(sum) dfs2(len+);
    }
}

int main()
{
    freopen("library.in","r",stdin);
    freopen("library.out","w",stdout);
    scanf("%s",s+);
    n=strlen(s+);
    for(int i=;i<=n;++i) cnt[s[i]-'a']++;
    dfs();
    dfs2();
    printf("%d",ans);
}