线段树（segment_tree)

线段树之——区间修改区间查询

1.概述

线段树，也叫区间树，是一个完全二叉树，它在各个节点保存一条线段（即“子数组”），因而常用于解决数列维护问题，基本能保证每个操作的复杂度为O(lgN)。

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

2.线段树基本操作

线段树的基本操作主要包括构造线段树，区间查询和区间修改。

（1）线段树构造

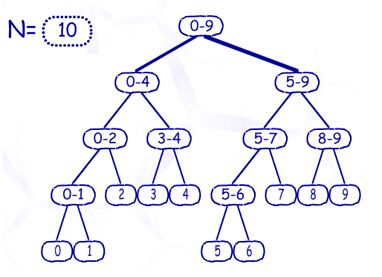
首先介绍构造线段树的方法：让根节点表示区间[0,N-1]，即所有N个数所组成的一个区间，然后，把区间分成两半，分别由左右子树表示。不难证明，这样的线段树的节点数只有2N-1个，是O(N)级别的，如图：

节点定义如下：

typedef struct node {
    int l;        //线段的左端点
    int r;        //线段的左端点
    int value;    //线段上的值
}node;

线段树的构建：

• 伪代码

  bulid//以节点v为根建树、v对应区间为[l,r]
  {
      对节点v初始化
       if (l!=r) {
            以v的左孩子为根建树，区间为[l,(l+r)/]
            以v的右孩子为根建树，区间为[(l+r)/+,r]
      }
  }

• 完整的建树代码

  #define N 10000
  node tree[N];
  void bulid(int l, int r, int v) //对结点v进行建立，区间为l~r
  {
      tree[v].l = l;
      tree[v].r = r;
      if(l == r) {
          //进行结点的初始化
          tree[v].value = a[r];
          return;
      }
      int mid = (l + r) / ;
      bulid(v * , l, mid);
      bulid(v *  + , mid + , r);
      //根据左右儿子更新当前结点
      tree[v].value = tree[v * ].value + tree[v *  + ].value;
  }

题目实现:

• 更新

  当在a[i]~a[j]上的所有的元素都加上一个值c的时候

  如果a[i]~a[j]刚还是一个完整段的时候，直接将这个段的value值加上c*(r-l+1)

  当更新的区间不是一个完整段的时候，采用一种记录增量的方法：给每个节点增加一个域：int add，记录更新操作的增量c，初始的时候add均为0，比如当对2~5区间更新后，给该结点的add加上一个值c，再下次要对2~3结点进行更新或查询时，再将add传递到下面的孩子结点中去

  完整的更新树代码如下:

  typedef struct node {
      int l;        //线段的左端点
      int r;        //线段的左端点
      int value;    //线段上的值
      int add;
  }node;
  void update(int v, int r, int l, int m)//更新区间l~r加上数m
  {
      if(tree[v].l == l && tree[v].r == r) {  //找到，更新并记录增量
          tree[v].value += m * (r - l + );
          tree[v].add = m;
          return;
      }
      if(tree[v].add) {
          tree[ * v].add += tree[v].add;
          tree[ * v + ].add += tree[v].add;
          tree[v].add = ;
      }
      int mid = (tree[v].l + tree[v].r) / ;
      if(r <= mid) {
          update(v * , l, r, m);   //只对左儿子更新
      } else {
          if(l > mid) {
              update(v *  + , l, r, m);  //只对右儿子更新
          } else {                        //区间横跨左右儿子区间，对其两者均进行更新
              update(v * , l, mid, m);
              update(v *  + , mid + , r, m);
          }
      }
  }

• 查询

　　  查询区间l~r上的value值

void query(int v, int l, int r)  //当前查询结点为v，要查询的区间为l~r
{
    if(tree[v].l == l && tree[v].r == r) {
        ans += tree[v].value;
        return;
    }
    if(tree[v].add) {
        tree[v * ].add += tree[v].add;
        tree[v *  + ].add += tree[v].add;
        tree[v].add = ;
    }
    int mid = (tree[v].l + tree[v].r) / ;
    if(r <= mid) {
        query(v * , l, r);   //要查询的区间都在左儿子
    } else {
        if(l > mid) {
            query(v *  + , l, r);  //要查询的区间都在左儿子
        } else {                //要查询的区间横跨左右孩子
            query(v * , l, mid);
            query(v *  + , mid + , r);
        }
    }
}

注:

　　源地址：http://www.cnblogs.com/archimedes/p/segment-tree.html