【堆】【洛谷例题】p1090 p1334 p1177

（都是比较简单的典型的而且都是小根堆的例题）

• p1090

合并果子【传送门】

算法分析：要尽量使用最小的体力合并完所有果子，那么每次合并的两堆果子应该是这所有堆中最小的一个（因为越先合并的堆要被算的次数越多），因此定义一个小根堆heap，每次合并最小（其实就是最上面的）的两堆，然后把这两堆的和再放入堆里，再次合并最小的两堆……直到合并完成。定义ans加上每次合并所需能量，最后输出ans；

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n,a,ans;
int heap[],heap_size;
int get(){
    int now,next,res;
    res=heap[];
    heap[]=heap[heap_size--];
    now=;
    while(now*<=heap_size){
        next=now*;
        if(next<heap_size&&heap[next+]<heap[next])next++;
        if(heap[now]<=heap[next])break;
        swap(heap[now],heap[next]);
        now=next;
    }
    return res;
}
void put(int d){
    int now,next;
    heap[++heap_size]=d;
    now=heap_size;
    while(now>){
        next=now/;
        if(heap[now]>=heap[next])break;
        swap(heap[now],heap[next]);
        now=next;
    }
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        cin>>a;
        put(a);
    }
    for(int i=;i<n;i++){
        int r1=get();
        int r2=get();
        ans+=(r1+r2);
        put(r1+r2);
    }
    cout<<ans<<endl;
}

---

• p1334

瑞瑞的木板【传送门】

这个题和上面的合并果子基本一毛一样qwq，真的可以一个代码过。

但是忍不住要吐槽一下：上面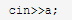我本来用的是scanf，结果评测

它wa掉了wa掉了！！！我改成cin过了qwq

---

• p1177

快速排序【传送门】

第一次ac（很久很久以前）sort过的

#include<bits/stdc++.h>
using namespace std;
int n;
int a[];
int main()
{
    cin>>n;
    for(int i=;i<=n;i++)
      cin>>a[i];
    sort(a+,a+n+);
    for(int i=;i<=n;i++)
    cout<<a[i]<<" ";
    return ;
}//防止头重脚轻，我们用万能头也好看一点qwq
（我是不会告诉你我是因为搞不懂哪个库对应什么才这么讲的）

学了堆以后，堆排序：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n,a,b;
int heap[],heap_size;
int get(){
    int now,next,res;
    res=heap[];
    heap[]=heap[heap_size--];
    now=;
    while(now*<=heap_size){
        next=now*;
        if(next<heap_size&&heap[next+]<heap[next])next++;
        if(heap[now]<=heap[next])break;
        swap(heap[now],heap[next]);
        now=next;
    }
    return res;
}
void put(int d){
    int now,next;
    heap[++heap_size]=d;
    now=heap_size;
    while(now>){
        next=now/;
        if(heap[now]>=heap[next])break;
        swap(heap[now],heap[next]);
        now=next;
    }
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d",&a);
        put(a);
    }
    for(int i=;i<n;i++)
        printf("%d ",get());
    printf("%d",get());
    return ;
}

end-