跳台阶（JAVA）

跳台阶
　　
　　

　　题目描述

　　一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

　　

　　思路：典型的动态规划问题，动态规划问题最关键的是把事件中的各种情形抽象为状态，然后找到前后状态之间的关系，写出状态转化方程，再翻译为代码。

　　　　可以考虑到题目中跳到第n层台阶有多少种跳法为一个状态，设置一个辅助数组dp[n+1]，dp[i]代表跳到第i层台阶的跳法总数。

　　　　因为一次只能跳1层或2层，那么dp[i]仅与dp[i-1]和dp[i-2]有关系。dp[i-1]可以通过跳一层得到dp[i]，而dp[i-2]可以通过跳两层得到dp[i]。

　　　　所以状态转化方程为：

　　　　　　　　dp[i] = dp[i-1]+dp[i-2];

　　　　

　　　　最后考虑边界条件：dp[1]= 1,dp[2] = 2;

　　　　

     public int JumpFloor(int target) {
         if(target<=2) return target;
         int[] dp = new int[target+1];
         dp[1] = 1;
         dp[2] = 2;
         for(int i=3;i<=target;i++){
             dp[i] = dp[i-1]+dp[i-2]*2;
         }
         return dp[target];
     }

　　　　

　跳台阶2

　　

　　一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
　　
　　思路：此时条件变化为一次可以跳n步，则dp[i]与前面的状态都有关系。有了上面的基础，可以轻松写出状态转移方程为：
　　　　

　　　　　　　　　　　　　　

　　

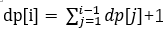
     public int JumpFloorII(int target) {
         if(target<=2) return target;
         int[] dp = new int[target+1];
         dp[1] = 1;
         dp[2] = 2;

         for(int i=3;i<=target;i++){
             //因为可以一步跳到
             dp[i] = 1;
             for(int j=1;j<i;j++){
                 dp[i] += dp[j];
             }
         }
         return dp[target];
     }