科学计算三维可视化---Mlab基础（数据可视化）

推文：科学计算三维可视化---TVTK库可视化实例

使用相关函数：科学计算三维可视化---Mlab基础（管线控制函数）

一：mlab.pipeline中标量数据可视化

通过持续实例，来感受mlab对数据可视化的方便性

（一）生成标量数据

等值面：（外层会覆盖内层）

import numpy as np
from mayavi import mlab

x,y,z = np.ogrid[-::20j,-::20j,-::20j]
s = np.sin(x*y*z)/(x*y*z)

mlab.contour3d(s)　　#等值面绘制
mlab.show()

切平面：

import numpy as np
from mayavi import mlab

x,y,z = np.ogrid[-::20j,-::20j,-::20j]
s = np.sin(x*y*z)/(x*y*z)

#绘制两个方向的切平面
mlab.pipeline.image_plane_widget(mlab.pipeline.scalar_field(s), #scalar_field获得数据的标量数据场
                                 plane_orientation="x_axes",    #设置切平面的方向
                                 slice_index=
                                 )

mlab.pipeline.image_plane_widget(mlab.pipeline.scalar_field(s),
                                 plane_orientation="y_axes",
                                 slice_index=
                                 )

#为这个数据绘制外框
mlab.outline()
mlab.show()

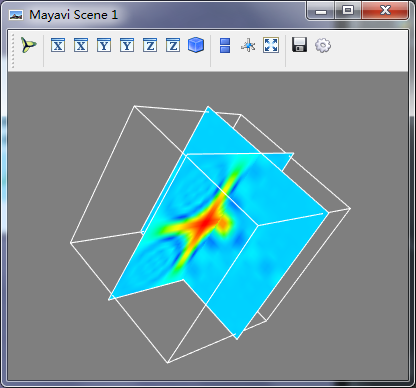
复合观测方法

import numpy as np
from mayavi import mlab

x,y,z = np.ogrid[-::20j,-::20j,-::20j]
s = np.sin(x*y*z)/(x*y*z)

src = mlab.pipeline.scalar_field(s) #建立标量场数据

mlab.pipeline.iso_surface(src,contours=[s.min()+0.1*s.ptp(),],opacity=0.1)  #iso_surface对输入体绘制其等值面，记得设置透明度，否则内部数据将被外部遮挡
mlab.pipeline.iso_surface(src,contours=[s.max()-0.1*s.ptp(),])  #也可以使用等值面iso_surface，来观察一定范围内的数据

#绘制切平面
mlab.pipeline.image_plane_widget(src,   #使用切平面来观察某一平面的数据细节
                                 plane_orientation="z_axes",    #设置切平面的方向
                                 slice_index=
                                 )

mlab.show()

二：mlab.pipeline中矢量数据可视化

import numpy as np
from mayavi import mlab

x,y,z = np.mgrid[::20j,::20j,::20j]

#u,v,w是在点x,y,z处的矢量数据
u = np.sin(np.pi*x)*np.cos(np.pi*z)
v = -*np.sin(np.pi*x)*np.cos(*np.pi*z)
w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(*np.pi*z)

mlab.quiver3d(u,v,w)    #quiver3d可以在数据点处画出箭头
mlab.outline()

mlab.show()

上面数据过于密集：可以使用降采样：科学计算三维可视化---TVTK库可视化实例 

import numpy as np
from mayavi import mlab

x,y,z = np.mgrid[::20j,::20j,::20j]

#u,v,w是在点x,y,z处的矢量数据
u = np.sin(np.pi*x)*np.cos(np.pi*z)
v = -*np.sin(np.pi*x)*np.cos(*np.pi*z)
w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(*np.pi*z)

src = mlab.pipeline.vector_field(u,v,w)
#pipeline的vectors构建了矢量域
mlab.pipeline.vectors(src,mask_points=10,scale_factor=2.0)  #mask_points没10个数据点选取一个，scale_factor放缩比率2.0

mlab.show()

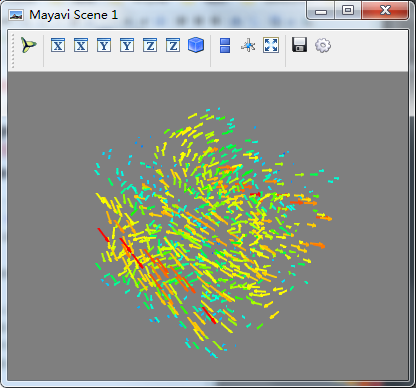
切面观察矢量数据

import numpy as np
from mayavi import mlab

x,y,z = np.mgrid[::20j,::20j,::20j]

#u,v,w是在点x,y,z处的矢量数据
u = np.sin(np.pi*x)*np.cos(np.pi*z)
v = -*np.sin(np.pi*x)*np.cos(*np.pi*z)
w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(*np.pi*z)

src = mlab.pipeline.vector_field(u,v,w)
#pipeline的vectors构建了矢量域
mlab.pipeline.vector_cut_plane(src,mask_points=10,scale_factor=2.0)  #mask_points没10个数据点选取一个，scale_factor放缩比率2.0

mlab.show()

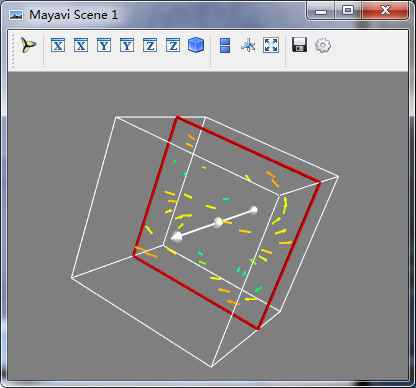
另一个矢量数据重要显示方法：级数的等值面

级数是矢量域中的重要参数，他可以显示数量的法线等值面，我们通过计算矢量法向得到一个标量域

import numpy as np
from mayavi import mlab

x,y,z = np.mgrid[::20j,::20j,::20j]

#u,v,w是在点x,y,z处的矢量数据
u = np.sin(np.pi*x)*np.cos(np.pi*z)
v = -*np.sin(np.pi*x)*np.cos(*np.pi*z)
w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(*np.pi*z)

src = mlab.pipeline.vector_field(u,v,w)
magnitude = mlab.pipeline.extract_vector_norm(src)  #extract_vector_norm通过计算矢量法向得到一个标量域
mlab.pipeline.iso_surface(magnitude,contours=[2.0,0.5]) #构建等值面

mlab.outline()
mlab.show()

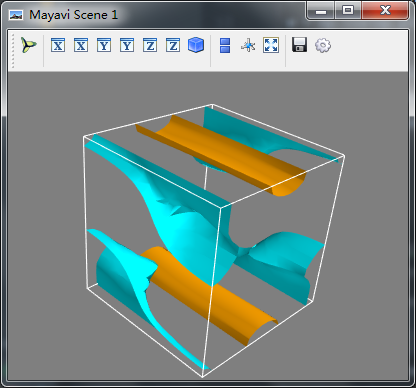
流线的可视化对矢量数据也非常有意义，在很多应用中，他可以表示流体力学的轨迹，有可以表示电磁场线

import numpy as np
from mayavi import mlab

x,y,z = np.mgrid[::20j,::20j,::20j]

#u,v,w是在点x,y,z处的矢量数据
u = np.sin(np.pi*x)*np.cos(np.pi*z)
v = -*np.sin(np.pi*x)*np.cos(*np.pi*z)
w = np.cos(np.pi*x)*np.sin(np.pi*z) + np.cos(np.pi*y)*np.sin(*np.pi*z)

flow = mlab.flow(u,v,w,seed_scale=,
                 seed_resolution=,
                 integration_direction="both")

mlab.outline()
mlab.show()

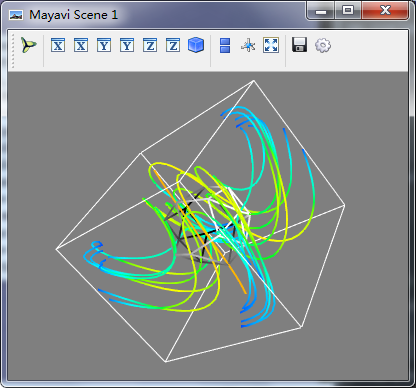
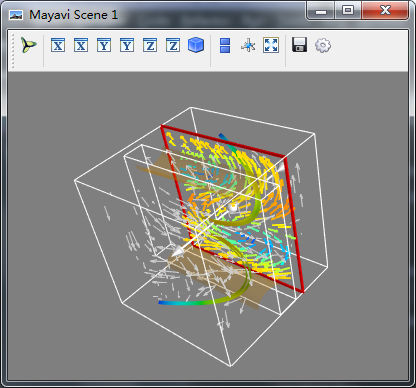
复合观测方法

为矢量场数据给出有意义的矢量观测是比较有困难的工作，因此通常我们需要使用不同的根据，对矢量数据进行可视化

#等值面
iso = mlab.pipeline.iso_surface(magnitude,contours=[2.0,],opacity=0.3) #构建等值面
#矢量场
vec = mlab.pipeline.vectors(magnitude,mask_points=,line_width=,
                            color=(0.8,0.8,0.8),
                            scale_factor=.)
#矢量场流线
flow = mlab.pipeline.streamline(magnitude,seedtype="plane",
                                seed_visible=False,
                                seed_scale=0.5,
                                seed_resolution=,
                                linetype="ribbon")
#矢量场切平面
vcp = mlab.pipeline.vector_cut_plane(magnitude,mask_points=,
                                     scale_factor=,
                                     colormap="jet",
                                     plane_orientation="x_axes")