[BZOJ3884] 上帝与集合的正确用法 (欧拉函数)

题目链接:  https://www.lydsy.com/JudgeOnline/problem.php?id=3884

题目大意：

给出 M, 求 $2^{2^{2^{2^{...}}}}$ % M 的值. p ≤ 1e9

题解：

我们设 M = $2^k$*p , p是奇数

$2^{2^{2^{2^{...}}}}$ % M =  $2^k$ * ($2^{2^{2^{2^{...}}}-k}$ % p)

因为p是奇数，所以p与2互质，我们可以用欧拉定理

原式化为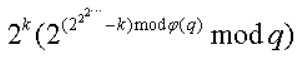

可以递归地做下去

但模数变成1的时候直接返回0就好了

参考某大佬博客的时间复杂度：

AC代码如下：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long ll;

int T;
inline int read()
{
    char ch=getchar();
    int s=,f=;
    while (!(ch>=''&&ch<='')) {if (ch=='-') f=-;ch=getchar();}
    while (ch>=''&&ch<='') {s=(s<<)+(s<<)+ch-'';ch=getchar();}
    return s*f;
}
int qpow(ll a,int b,int m)
{
    ll res=;
    for (;b;b>>=,a=a*a%m) if (b&) res=res*a%m;
    return res%m;
}
int phi(int x)
{
    int res=x;
    for (int i=;i*i<=x;i++)
    {
        if (x%i) continue;
        res/=i;res*=i-;
        while (x%i==) x/=i;
    }
    if (x>) res/=x,res*=x-;
    return res;
}
int solve(int p)
{
    if (p==) return ;
    int k=;
    while (~p&) p>>=,k++;
    int phi_p=phi(p);
    int re=solve(phi_p);
    re=(re+phi_p-k%phi_p)%phi_p;
    re=qpow(,re,p);
    return re<<k;
}
int main()
{
    T=read();
    while (T--)
    {
        int p=read();
        printf("%d\n",solve(p));
    }
    return ;
}